2008:Audio Classical Composer Identification Results
Contents
- 1 Introduction
- 2 Overall Summary Results
Introduction
These are the results for the 2008 running of the Audio Classical Composer Identification task. For background information about this task set please refer to the 2007:Audio Classical Composer Identification page.
The data set consisted of 2772 30 second audio clips. The composers represented were:
- Bach
- Beethoven
- Brahms
- Chopin
- Dvorak
- Handel
- Haydn
- Mendelssohnn
- Mozart
- Schubert
- Vivaldi
The goal was to correctly identify the composer who wrote each of the pieces represented.
General Legend
Team ID
GP1 = G. Peeters
GT1 = G. Tzanetakis
GT2 = G. Tzanetakis
GT3 = G. Tzanetakis
LRPPI1 = T. Lidy, A. Rauber, A. Pertusa, P. Peonce de León, J. M. Iñesta 1
LRPPI2 = T. Lidy, A. Rauber, A. Pertusa, P. Peonce de León, J. M. Iñesta 2
LRPPI3 = T. Lidy, A. Rauber, A. Pertusa, P. Peonce de León, J. M. Iñesta 3
LRPPI4 = T. Lidy, A. Rauber, A. Pertusa, P. Peonce de León, J. M. Iñesta 4
ME1 = M. I. Mandel, D. P. W. Ellis 1
ME2 = M. I. Mandel, D. P. W. Ellis 2
ME3 = M. I. Mandel, D. P. W. Ellis 3
Overall Summary Results
MIREX 2008 Audio Classical Composer Classification Summary Results - Raw Classification Accuracy Averaged Over Three Train/Test Folds
| Participant | Average Classifcation Accuracy |
|---|---|
| GP1 | 48.99% |
| GT1 | 39.47% |
| GT2 | 45.82% |
| GT3 | 43.81% |
| LRPPI1 | 34.13% |
| LRPPI2 | 39.43% |
| LRPPI3 | 37.48% |
| LRPPI4 | 39.54% |
| ME1 | 53.25% |
| ME2 | 53.10% |
| ME3 | 52.89% |
Accuracy Across Folds
| Classification fold | GP1 | GT1 | GT2 | GT3 | LRPPI1 | LRPPI2 | LRPPI3 | LRPPI4 | ME1 | ME2 | ME3 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.501 | 0.363 | 0.452 | 0.457 | 0.165 | 0.386 | 0.379 | 0.389 | 0.545 | 0.538 | 0.532 |
| 1 | 0.483 | 0.415 | 0.464 | 0.424 | 0.431 | 0.406 | 0.369 | 0.395 | 0.523 | 0.525 | 0.527 |
| 2 | 0.486 | 0.407 | 0.458 | 0.433 | 0.429 | 0.391 | 0.377 | 0.403 | 0.529 | 0.530 | 0.527 |
Accuracy Across Categories
| Class | GP1 | GT1 | GT2 | GT3 | LRPPI1 | LRPPI2 | LRPPI3 | LRPPI4 | ME1 | ME2 | ME3 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| bach | 0.667 | 0.516 | 0.651 | 0.571 | 0.563 | 0.575 | 0.500 | 0.583 | 0.734 | 0.738 | 0.738 |
| beethoven | 0.321 | 0.409 | 0.548 | 0.425 | 0.198 | 0.310 | 0.266 | 0.282 | 0.393 | 0.385 | 0.393 |
| brahms | 0.290 | 0.159 | 0.198 | 0.230 | 0.198 | 0.321 | 0.310 | 0.310 | 0.429 | 0.429 | 0.433 |
| chopin | 0.913 | 0.885 | 0.897 | 0.810 | 0.595 | 0.663 | 0.627 | 0.659 | 0.770 | 0.774 | 0.766 |
| dvorak | 0.417 | 0.333 | 0.488 | 0.484 | 0.393 | 0.369 | 0.393 | 0.361 | 0.456 | 0.444 | 0.448 |
| handel | 0.492 | 0.310 | 0.302 | 0.321 | 0.397 | 0.425 | 0.377 | 0.405 | 0.548 | 0.548 | 0.544 |
| haydn | 0.655 | 0.488 | 0.651 | 0.556 | 0.369 | 0.413 | 0.397 | 0.460 | 0.603 | 0.607 | 0.603 |
| mendelssohnn | 0.337 | 0.472 | 0.492 | 0.401 | 0.286 | 0.401 | 0.306 | 0.341 | 0.488 | 0.472 | 0.468 |
| mozart | 0.266 | 0.087 | 0.079 | 0.242 | 0.234 | 0.246 | 0.274 | 0.214 | 0.353 | 0.353 | 0.345 |
| schubert | 0.302 | 0.194 | 0.230 | 0.210 | 0.175 | 0.218 | 0.262 | 0.278 | 0.417 | 0.425 | 0.425 |
| vivaldi | 0.730 | 0.488 | 0.504 | 0.567 | 0.345 | 0.397 | 0.413 | 0.456 | 0.667 | 0.667 | 0.655 |
MIREX 2008 Audio Classical Composer Classification Evaluation Logs and Confusion Matrices
MIREX 2008 Audio Classical Composer Classification Run Times
| Participant | Runtime (hh:mm) / Fold |
|---|---|
| GP1 | Feat Ex: 04:40 Train/Classify: 00:47 |
| GT1 | Feat Ex/Train/Classify: 00:16 |
| GT2 | Feat Ex/Train/Classify: 00:34 |
| GT3 | Feat Ex: 00:05 Train/Classify: 00:00 (7 sec) |
| LRPPI1 | Feat Ex: 08:00 Train/Classify: 00:02 |
| LRPPI2 | Feat Ex: 08:00 Train/Classify: 00:09 |
| LRPPI3 | Feat Ex: 08:00 Train/Classify: 00:09 |
| LRPPI4 | Feat Ex: 08:00 Train/Classify: 00:14 |
| ME1 | Feat Ex: 1:17 Train/Classify: 00:00 (21 sec) |
| ME2 | Feat Ex: 1:17 Train/Classify: 00:00 (21 sec) |
| ME3 | Feat Ex: 1:17 Train/Classify: 00:00 (21 sec) |
CSV Files Without Rounding
audiocomposer_results_fold.csv
audiocomposer_results_class.csv
Results By Algorithm
(.tar.gz)
GP1 = G. Peeters
GT1 = G. Tzanetakis
GT2 = G. Tzanetakis
GT3 = G. Tzanetakis
LRPPI1 = T. Lidy, A. Rauber, A. Pertusa, P. Peonce de León, J. M. Iñesta 1
LRPPI2 = T. Lidy, A. Rauber, A. Pertusa, P. Peonce de León, J. M. Iñesta 2
LRPPI3 = T. Lidy, A. Rauber, A. Pertusa, P. Peonce de León, J. M. Iñesta 3
LRPPI4 = T. Lidy, A. Rauber, A. Pertusa, P. Peonce de León, J. M. Iñesta 4
ME1 = I. M. Mandel, D. P. W. Ellis 1
ME2 = I. M. Mandel, D. P. W. Ellis 2
ME3 = I. M. Mandel, D. P. W. Ellis 3
Friedman's Test for Significant Differences
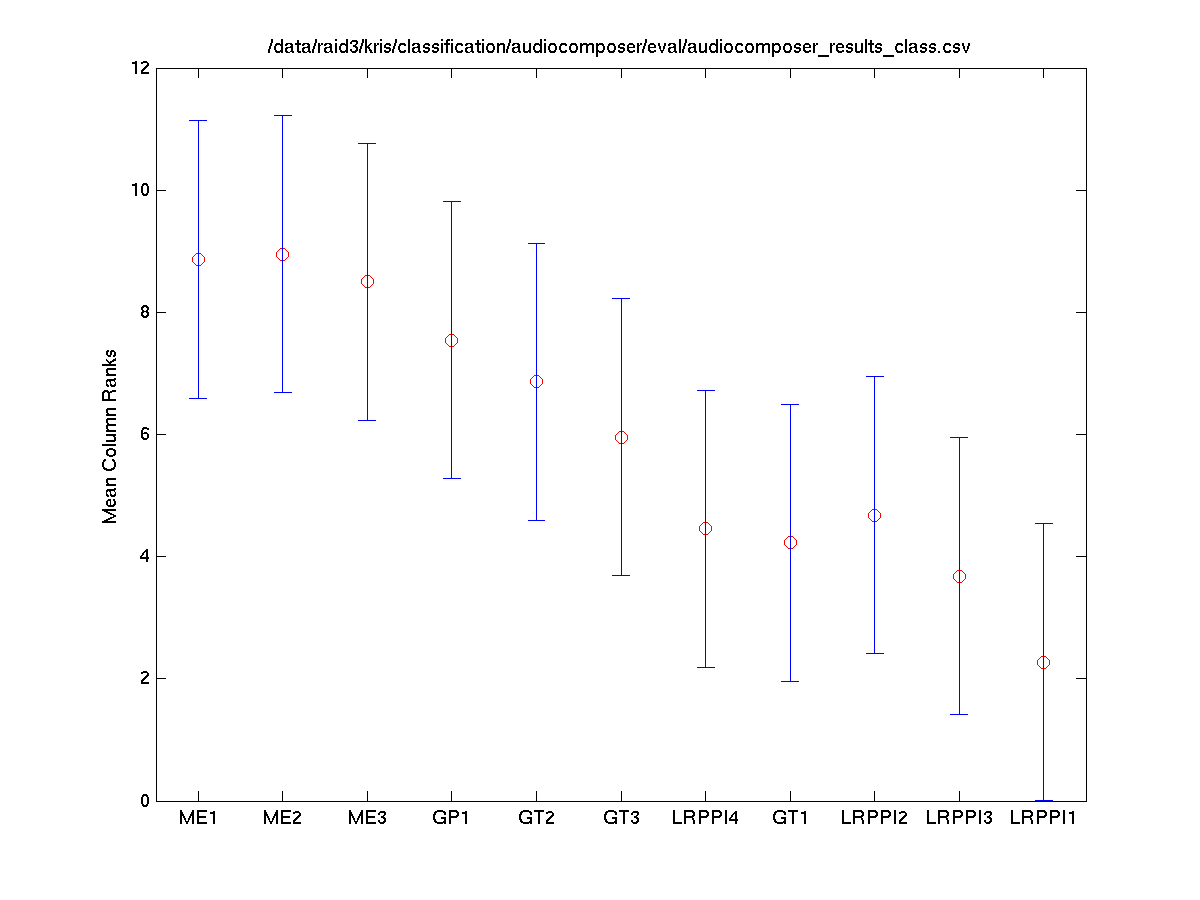
Classes vs. Systems
The Friedman test was run in MATLAB against the average accuracy for each class.
Friedman's Anova Table
| Source | SS | df | MS | Chi-sq | Prob>Chi-sq |
|---|---|---|---|---|---|
| Columns | 581.36 | 10 | 58.1364 | 53.09 | 7.16E-08 |
| Error | 623.14 | 100 | 6.2314 | ||
| Total | 1204.5 | 120 |
Tukey-Kramer HSD Multi-Comparison
The Tukey-Kramer HSD multi-comparison data below was generated using the following MATLAB instruction. Command: [c, m, h, gnames] = multicompare(stats, 'ctype', 'tukey-kramer', 'estimate', 'friedman', 'alpha', 0.05);
| TeamID | TeamID | Lowerbound | Mean | Upperbound | Significance |
|---|---|---|---|---|---|
| GP1 | GT1 | -4.6324 | -0.0909 | 4.4506 | FALSE |
| GP1 | GT2 | -4.1779 | 0.3636 | 4.9051 | FALSE |
| GP1 | GT3 | -3.2233 | 1.3182 | 5.8597 | FALSE |
| GP1 | LRPPI1 | -2.5415 | 2.0000 | 6.5415 | FALSE |
| GP1 | LRPPI2 | -1.6324 | 2.9091 | 7.4506 | FALSE |
| GP1 | LRPPI3 | -0.1324 | 4.4091 | 8.9506 | FALSE |
| GP1 | LRPPI4 | 0.0949 | 4.6364 | 9.1779 | TRUE |
| GP1 | ME1 | -0.3597 | 4.1818 | 8.7233 | FALSE |
| GP1 | ME2 | 0.6403 | 5.1818 | 9.7233 | TRUE |
| GP1 | ME3 | 2.0494 | 6.5909 | 11.1324 | TRUE |
| GT1 | GT2 | -4.0870 | 0.4545 | 4.9961 | FALSE |
| GT1 | GT3 | -3.1324 | 1.4091 | 5.9506 | FALSE |
| GT1 | LRPPI1 | -2.4506 | 2.0909 | 6.6324 | FALSE |
| GT1 | LRPPI2 | -1.5415 | 3.0000 | 7.5415 | FALSE |
| GT1 | LRPPI3 | -0.0415 | 4.5000 | 9.0415 | FALSE |
| GT1 | LRPPI4 | 0.1858 | 4.7273 | 9.2688 | TRUE |
| GT1 | ME1 | -0.2688 | 4.2727 | 8.8142 | FALSE |
| GT1 | ME2 | 0.7312 | 5.2727 | 9.8142 | TRUE |
| GT1 | ME3 | 2.1403 | 6.6818 | 11.2233 | TRUE |
| GT2 | GT3 | -3.5870 | 0.9545 | 5.4961 | FALSE |
| GT2 | LRPPI1 | -2.9051 | 1.6364 | 6.1779 | FALSE |
| GT2 | LRPPI2 | -1.9961 | 2.5455 | 7.0870 | FALSE |
| GT2 | LRPPI3 | -0.4961 | 4.0455 | 8.5870 | FALSE |
| GT2 | LRPPI4 | -0.2688 | 4.2727 | 8.8142 | FALSE |
| GT2 | ME1 | -0.7233 | 3.8182 | 8.3597 | FALSE |
| GT2 | ME2 | 0.2767 | 4.8182 | 9.3597 | TRUE |
| GT2 | ME3 | 1.6858 | 6.2273 | 10.7688 | TRUE |
| GT3 | LRPPI1 | -3.8597 | 0.6818 | 5.2233 | FALSE |
| GT3 | LRPPI2 | -2.9506 | 1.5909 | 6.1324 | FALSE |
| GT3 | LRPPI3 | -1.4506 | 3.0909 | 7.6324 | FALSE |
| GT3 | LRPPI4 | -1.2233 | 3.3182 | 7.8597 | FALSE |
| GT3 | ME1 | -1.6779 | 2.8636 | 7.4051 | FALSE |
| GT3 | ME2 | -0.6779 | 3.8636 | 8.4051 | FALSE |
| GT3 | ME3 | 0.7312 | 5.2727 | 9.8142 | TRUE |
| LRPPI1 | LRPPI2 | -3.6324 | 0.9091 | 5.4506 | FALSE |
| LRPPI1 | LRPPI3 | -2.1324 | 2.4091 | 6.9506 | FALSE |
| LRPPI1 | LRPPI4 | -1.9051 | 2.6364 | 7.1779 | FALSE |
| LRPPI1 | ME1 | -2.3597 | 2.1818 | 6.7233 | FALSE |
| LRPPI1 | ME2 | -1.3597 | 3.1818 | 7.7233 | FALSE |
| LRPPI1 | ME3 | 0.0494 | 4.5909 | 9.1324 | TRUE |
| LRPPI2 | LRPPI3 | -3.0415 | 1.5000 | 6.0415 | FALSE |
| LRPPI2 | LRPPI4 | -2.8142 | 1.7273 | 6.2688 | FALSE |
| LRPPI2 | ME1 | -3.2688 | 1.2727 | 5.8142 | FALSE |
| LRPPI2 | ME2 | -2.2688 | 2.2727 | 6.8142 | FALSE |
| LRPPI2 | ME3 | -0.8597 | 3.6818 | 8.2233 | FALSE |
| LRPPI3 | LRPPI4 | -4.3142 | 0.2273 | 4.7688 | FALSE |
| LRPPI3 | ME1 | -4.7688 | -0.2273 | 4.3142 | FALSE |
| LRPPI3 | ME2 | -3.7688 | 0.7727 | 5.3142 | FALSE |
| LRPPI3 | ME3 | -2.3597 | 2.1818 | 6.7233 | FALSE |
| LRPPI4 | ME1 | -4.9961 | -0.4545 | 4.0870 | FALSE |
| LRPPI4 | ME2 | -3.9961 | 0.5455 | 5.0870 | FALSE |
| LRPPI4 | ME3 | -2.5870 | 1.9545 | 6.4961 | FALSE |
| ME1 | ME2 | -3.5415 | 1.0000 | 5.5415 | FALSE |
| ME1 | ME3 | -2.1324 | 2.4091 | 6.9506 | FALSE |
| ME2 | ME3 | -3.1324 | 1.4091 | 5.9506 | FALSE |
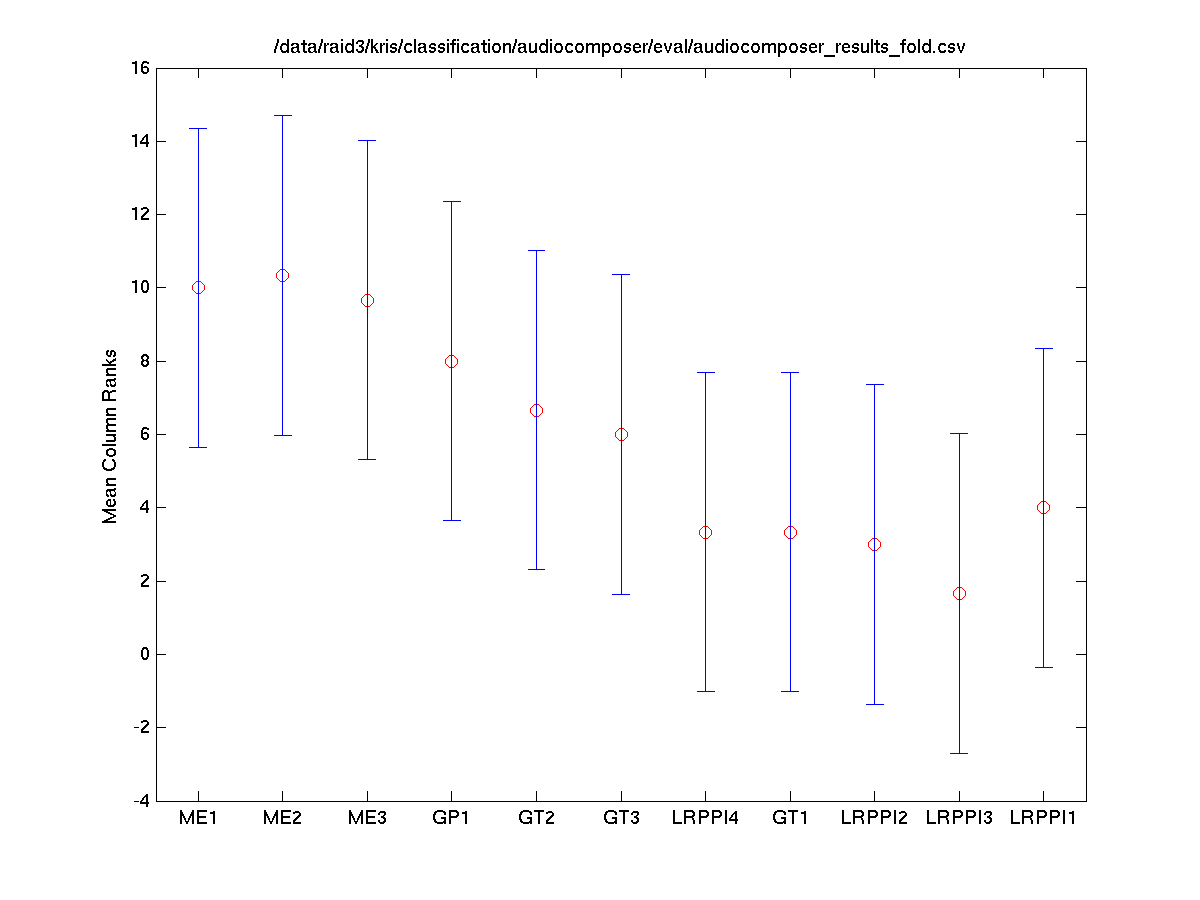
Folds vs. Systems
The Friedman test was run in MATLAB against the accuracy for each fold.
Friedman's Anova Table
| Source | SS | df | MS | Chi-sq | Prob>Chi-sq |
|---|---|---|---|---|---|
| Columns | 296 | 10 | 29.6 | 26.91 | 0.0027 |
| Error | 34 | 20 | 1.7 | ||
| Total | 330 | 32 |
Tukey-Kramer HSD Multi-Comparison
The Tukey-Kramer HSD multi-comparison data below was generated using the following MATLAB instruction. Command: [c, m, h, gnames] = multicompare(stats, 'ctype', 'tukey-kramer', 'estimate', 'friedman', 'alpha', 0.05);
| TeamID | TeamID | Lowerbound | Mean | Upperbound | Significance |
|---|---|---|---|---|---|
| GP1 | GT1 | -9.0495 | -0.3333 | 8.3828 | FALSE |
| GP1 | GT2 | -8.3828 | 0.3333 | 9.0495 | FALSE |
| GP1 | GT3 | -6.7162 | 2.0000 | 10.7162 | FALSE |
| GP1 | LRPPI1 | -5.3828 | 3.3333 | 12.0495 | FALSE |
| GP1 | LRPPI2 | -4.7162 | 4.0000 | 12.7162 | FALSE |
| GP1 | LRPPI3 | -2.0495 | 6.6667 | 15.3828 | FALSE |
| GP1 | LRPPI4 | -2.0495 | 6.6667 | 15.3828 | FALSE |
| GP1 | ME1 | -1.7162 | 7.0000 | 15.7162 | FALSE |
| GP1 | ME2 | -0.3828 | 8.3333 | 17.0495 | FALSE |
| GP1 | ME3 | -2.7162 | 6.0000 | 14.7162 | FALSE |
| GT1 | GT2 | -8.0495 | 0.6667 | 9.3828 | FALSE |
| GT1 | GT3 | -6.3828 | 2.3333 | 11.0495 | FALSE |
| GT1 | LRPPI1 | -5.0495 | 3.6667 | 12.3828 | FALSE |
| GT1 | LRPPI2 | -4.3828 | 4.3333 | 13.0495 | FALSE |
| GT1 | LRPPI3 | -1.7162 | 7.0000 | 15.7162 | FALSE |
| GT1 | LRPPI4 | -1.7162 | 7.0000 | 15.7162 | FALSE |
| GT1 | ME1 | -1.3828 | 7.3333 | 16.0495 | FALSE |
| GT1 | ME2 | -0.0495 | 8.6667 | 17.3828 | FALSE |
| GT1 | ME3 | -2.3828 | 6.3333 | 15.0495 | FALSE |
| GT2 | GT3 | -7.0495 | 1.6667 | 10.3828 | FALSE |
| GT2 | LRPPI1 | -5.7162 | 3.0000 | 11.7162 | FALSE |
| GT2 | LRPPI2 | -5.0495 | 3.6667 | 12.3828 | FALSE |
| GT2 | LRPPI3 | -2.3828 | 6.3333 | 15.0495 | FALSE |
| GT2 | LRPPI4 | -2.3828 | 6.3333 | 15.0495 | FALSE |
| GT2 | ME1 | -2.0495 | 6.6667 | 15.3828 | FALSE |
| GT2 | ME2 | -0.7162 | 8.0000 | 16.7162 | FALSE |
| GT2 | ME3 | -3.0495 | 5.6667 | 14.3828 | FALSE |
| GT3 | LRPPI1 | -7.3828 | 1.3333 | 10.0495 | FALSE |
| GT3 | LRPPI2 | -6.7162 | 2.0000 | 10.7162 | FALSE |
| GT3 | LRPPI3 | -4.0495 | 4.6667 | 13.3828 | FALSE |
| GT3 | LRPPI4 | -4.0495 | 4.6667 | 13.3828 | FALSE |
| GT3 | ME1 | -3.7162 | 5.0000 | 13.7162 | FALSE |
| GT3 | ME2 | -2.3828 | 6.3333 | 15.0495 | FALSE |
| GT3 | ME3 | -4.7162 | 4.0000 | 12.7162 | FALSE |
| LRPPI1 | LRPPI2 | -8.0495 | 0.6667 | 9.3828 | FALSE |
| LRPPI1 | LRPPI3 | -5.3828 | 3.3333 | 12.0495 | FALSE |
| LRPPI1 | LRPPI4 | -5.3828 | 3.3333 | 12.0495 | FALSE |
| LRPPI1 | ME1 | -5.0495 | 3.6667 | 12.3828 | FALSE |
| LRPPI1 | ME2 | -3.7162 | 5.0000 | 13.7162 | FALSE |
| LRPPI1 | ME3 | -6.0495 | 2.6667 | 11.3828 | FALSE |
| LRPPI2 | LRPPI3 | -6.0495 | 2.6667 | 11.3828 | FALSE |
| LRPPI2 | LRPPI4 | -6.0495 | 2.6667 | 11.3828 | FALSE |
| LRPPI2 | ME1 | -5.7162 | 3.0000 | 11.7162 | FALSE |
| LRPPI2 | ME2 | -4.3828 | 4.3333 | 13.0495 | FALSE |
| LRPPI2 | ME3 | -6.7162 | 2.0000 | 10.7162 | FALSE |
| LRPPI3 | LRPPI4 | -8.7162 | 0.0000 | 8.7162 | FALSE |
| LRPPI3 | ME1 | -8.3828 | 0.3333 | 9.0495 | FALSE |
| LRPPI3 | ME2 | -7.0495 | 1.6667 | 10.3828 | FALSE |
| LRPPI3 | ME3 | -9.3828 | -0.6667 | 8.0495 | FALSE |
| LRPPI4 | ME1 | -8.3828 | 0.3333 | 9.0495 | FALSE |
| LRPPI4 | ME2 | -7.0495 | 1.6667 | 10.3828 | FALSE |
| LRPPI4 | ME3 | -9.3828 | -0.6667 | 8.0495 | FALSE |
| ME1 | ME2 | -7.3828 | 1.3333 | 10.0495 | FALSE |
| ME1 | ME3 | -9.7162 | -1.0000 | 7.7162 | FALSE |
| ME2 | ME3 | -11.0495 | -2.3333 | 6.3828 | FALSE |