2014:Discovery of Repeated Themes & Sections Results

Introduction

THIS PAGE IS STILL UNDER CONSTRUCTION. At present it just contains a copy of last year's results. If you are looking for the 2014 results, please check back here again on Thu 23 October.

The task: algorithms take a piece of music as input, and output a list of patterns repeated within that piece. A pattern is defined as a set of ontime-pitch pairs that occurs at least twice (i.e., is repeated at least once) in a piece of music. The second, third, etc. occurrences of the pattern will likely be shifted in time and/or transposed, relative to the first occurrence. Ideally an algorithm will be able to discover all exact and inexact occurrences of a pattern within a piece, so in evaluating this task we are interested in both:

(1) to what extent an algorithm can discover one occurrence, up to time shift and transposition, and;
(2) to what extent it can find all occurrences.

The metrics establishment recall, establishment precision and establishment F1 address (1), and the metrics occurrence recall, occurrence precision, and occurrence F1 address (2).

Contribution

Existing approaches to music structure analysis in MIR tend to focus on segmentation (e.g., Weiss & Bello, 2010). The contribution of this task is to afford access to the note content itself (please see the example in Fig. 1A), requiring algorithms to do more than label time windows (e.g., the segmentations in Figs. 1B-D). For instance, a discovery algorithm applied to the piece in Fig. 1A should return a pattern corresponding to the note content of $P_{1}$ and $P_{2}$ , as well as a pattern corresponding to the note content of $Q_{1}$ . This is because $Q_{1}$ occurs again independently of the accompaniment in bars 19-22 (not shown here). The ground truth also contains nested patterns, such as $P_{1}$ in Fig. 1A being a subset of the sectional repetition $S_{1}$ , reflecting the often-hierarchical nature of musical repetition. While we recognise the appealing simplicity of linear segmentation, in the Discovery of Repeated Themes & Sections task we are demanding analysis at a greater level of detail, and have built a ground truth that contains overlapping and nested patterns.

Figure 1. Pattern discovery v segmentation. (A) Bars 1-12 of Mozart’s Piano Sonata in E-flat major K282 mvt.2, showing some ground-truth themes and repeated sections; (B-D) Three linear segmentations. Numbers below the staff in Fig. 1A and below the segmentation in Fig. 1D indicate crotchet beats, from zero for bar 1 beat 1.

For a more detailed introduction to the task, please see 2014:Discovery_of_Repeated_Themes_&_Sections.

Ground Truth and Algorithms

The ground truth, called the Johannes Kepler University Patterns Test Database (JKUPTD-Aug2013), is based on motifs and themes in Barlow and Morgenstern (1953), Schoenberg (1967), and Bruhn (1993). Repeated sections are based on those marked by the composer. These annotations are supplemented with some of our own where necessary. A Development Database (JKUPDD-Aug2013) enabled participants to try out their algorithms. For each piece in the Development and Test Databases, symbolic and synthesised audio versions are crossed with monophonic and polyphonic versions, giving four versions of the task in total: symPoly, symMono, audPoly, and audMono. Algorithms submitted to the task are are shown in Table 1.

Sub code	Submission name	Abstract	Contributors
Task Version	symMono
NF1	MotivesExtractor	PDF	Oriol Nieto, Morwaread Farbood
OL1	PatMinr	PDF	Olivier Lartillot
VM1	VM1	PDF	Gissel Velarde, David Meredith
VM2	VM2	PDF	Gissel Velarde, David Meredith
NF1'13	motives_mono	PDF	Oriol Nieto, Morwaread Farbood
DM10'13	SIATECCompressSegment	PDF	David Meredith
Task Version	symPoly
NF1	MotivesExtractor	PDF	Oriol Nieto, Morwaread Farbood
NF2'13	motives_poly	PDF	Oriol Nieto, Morwaread Farbood
DM10'13	SIATECCompressSegment	PDF	David Meredith
Task Version	audMono
NF1	MotivesExtractor	PDF	Oriol Nieto, Morwaread Farbood
NF3'13	motives_audio_mono	PDF	Oriol Nieto, Morwaread Farbood
Task Version	audPoly
NF1	MotivesExtractor	PDF	Oriol Nieto, Morwaread Farbood
NF4'13	motives_audio_poly	PDF	Oriol Nieto, Morwaread Farbood

Table 1. Algorithms submitted to DRTS. Strong-performing algorithms from 2013 (submission codes ending '13) are included for the sake of extra comparisons.

Results

For mathematical definitions of the various metrics, please see 2014:Discovery_of_Repeated_Themes_&_Sections#Evaluation_Procedure.

In Brief

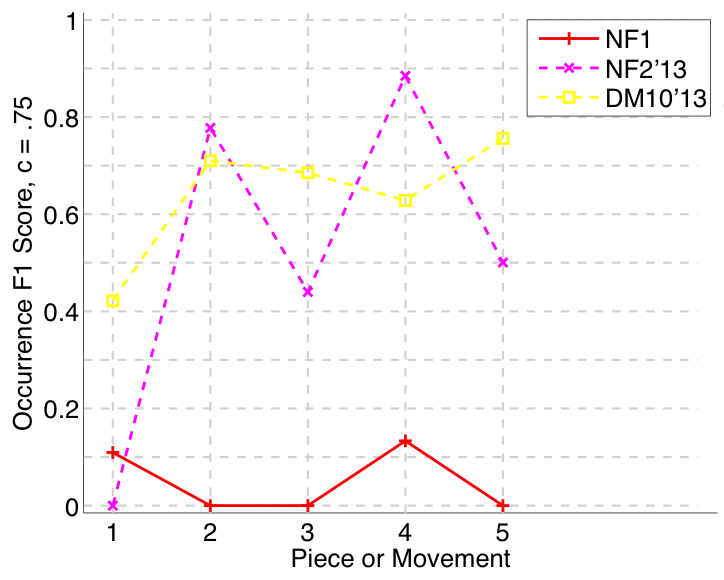
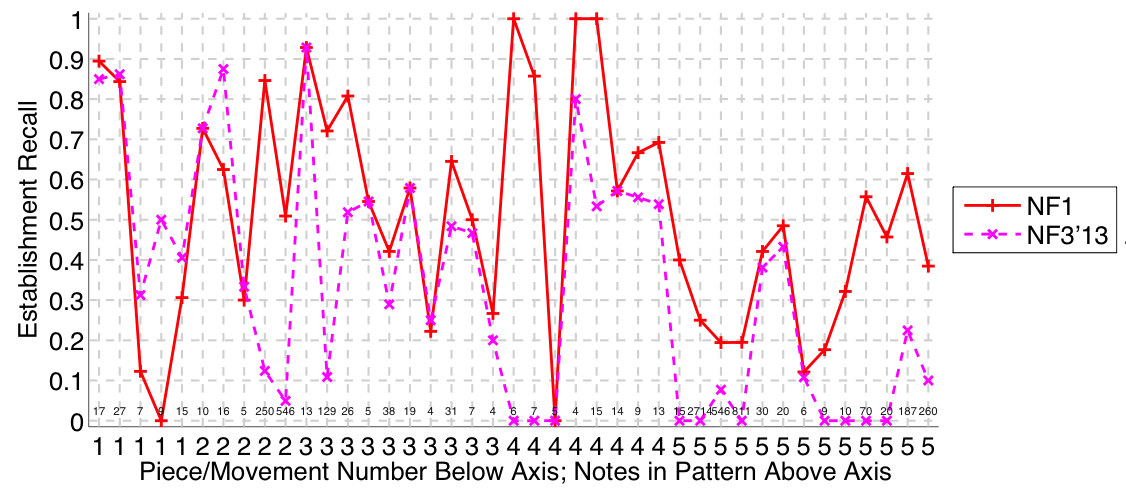
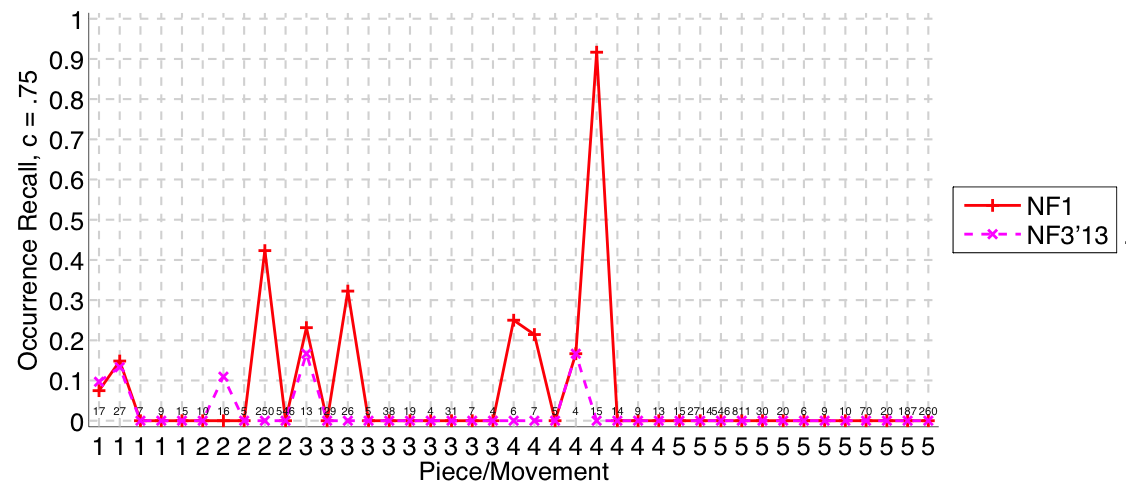
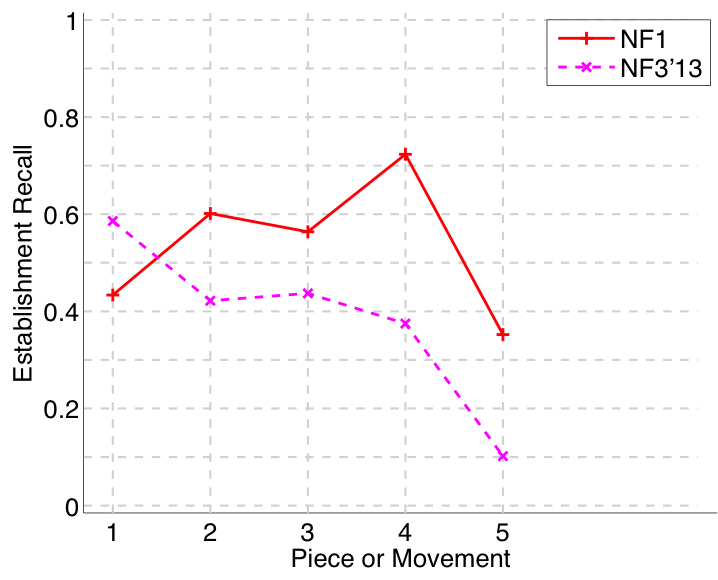
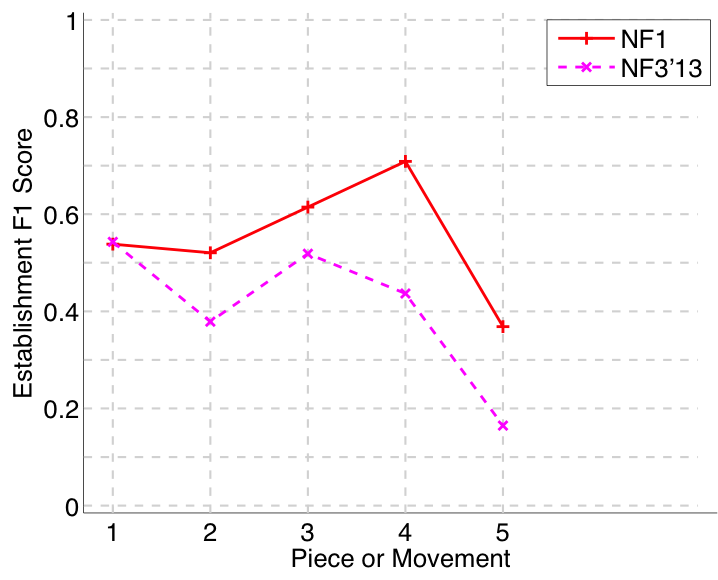
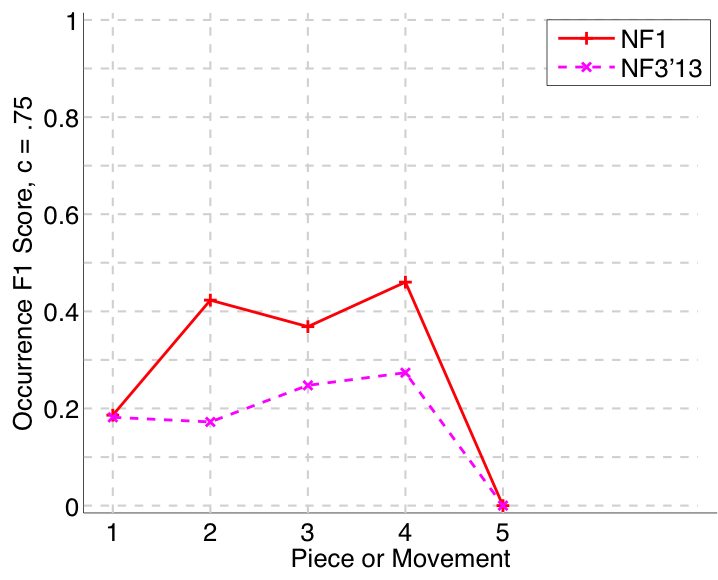
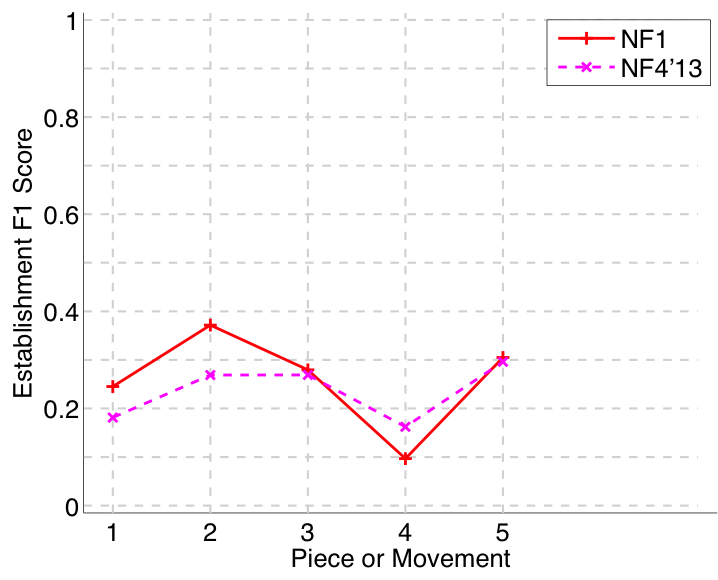
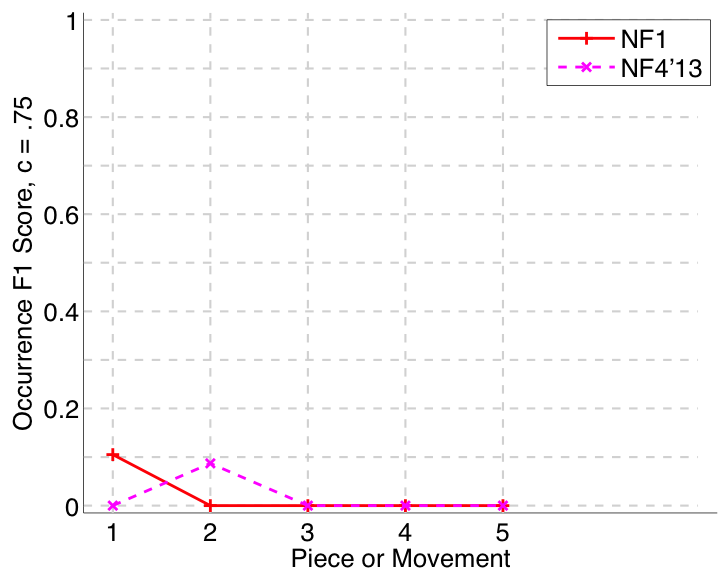
Nieto and Farbood (2014a) submitted to all four versions of the task (symbolic-monophonic, symbolic-polyphonic, audio-monophonic, audio-polyphonic), as they did last year (Nieto and Farbood, 2013). On the audio-monophonic version of the task, their NF1 algorithm’s $F_{1}$ scores were up by an average of .14 (establishing at least one occurrence of each ground truth pattern) and .11 (retrieving all occurrences of a discovered ground truth pattern) compared to last year (see Figs. 30 and 33). There were slighter increases in the audio-polyphonic version of the task. Their work on extracting repetitive structure remains at the forefront of research attempting to cross the audio-symbolic divide (Nieto & Farbood, 2014b; Collins et al., 2014).

Lartillot (2014a, 2014b) submitted an incremental pattern mining algorithm to the symbolic-monophonic version of the task this year. The musical dimensions represented (e.g., chromatic pitch, diatonic pitch) are able to vary throughout the course of a pattern occurrence. The ability to vary representation within an occurrence should mean that Lartillot’s OL1 algorithm is well prepared for retrieving both exact and inexact occurrences of motifs and themes. This does seem to be the case, with OL1 the strongest performer on the occurrence $F_{1}$ metric (Fig. 9).

Velarde and Meredith (2014) submitted a wavelet-based method to the symbolic-monophonic version of the task this year. This algorithm, VM1, tested significantly stronger according to Friedman's test than NF1 ( $\chi ^{2}(1)=25,\ p<.001$ , Bonferroni-corrected) and OL1 ( $\chi ^{2}(1)=17.86,\ p<.001$ , Bonferroni-corrected) at discovering at least one occurrence of each ground truth pattern (Fig. 2). While VM1 also seems to find lots of occurrences of each ground truth pattern (with high occurrence recall in Figs. 7, and 3 on a per-pattern basis), it may also find quite a few false-positive occurrences (with lower occurrence precision in Fig. 8). (To avoid a bias toward the more numerous submissions of Velarde and Meredith (2014), VM1 was preselected for comparison with Nieto and Farbood's (2014a) and Lartillot's (2014a) submissions, based on performance for the Development Database.)

symMono

(Submission OL1 did not complete on piece 5. The task captain took the decision to assign the mean of the evaluation metrics for OL1 calculated across the remaining pieces.)

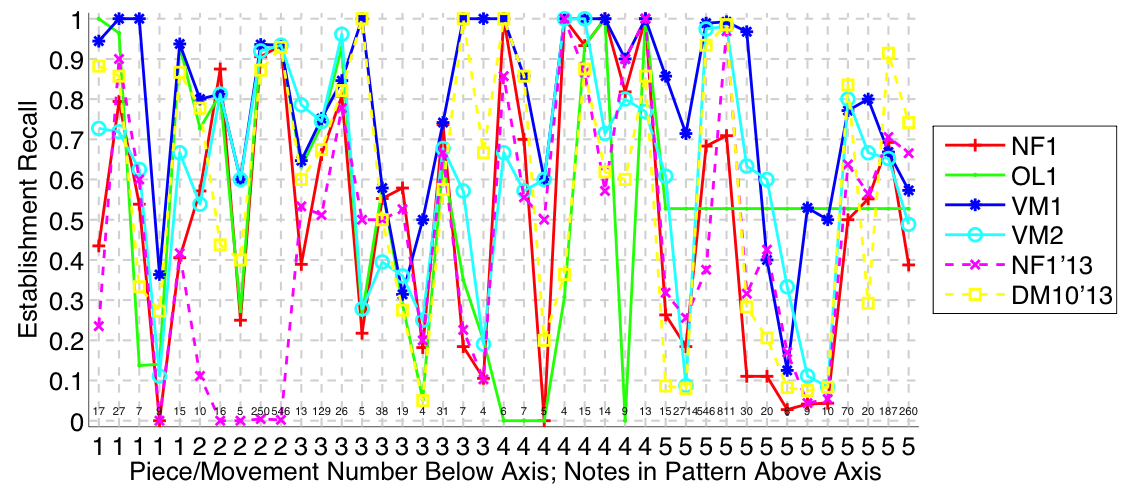
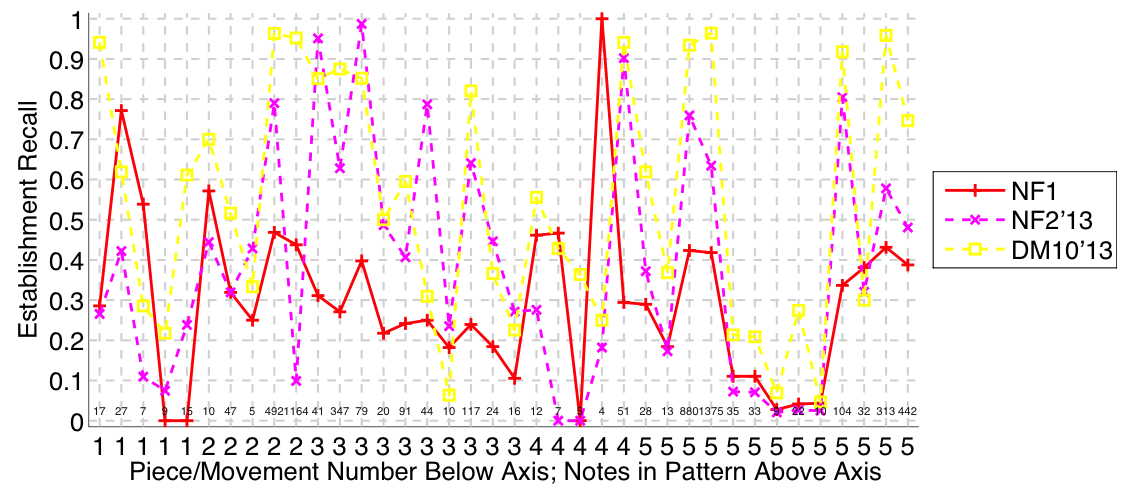
Figure 2. Establishment recall on a per-pattern basis. Establishment recall answers the following question. On average, how similar is the most similar algorithm-output pattern to a ground-truth pattern prototype?

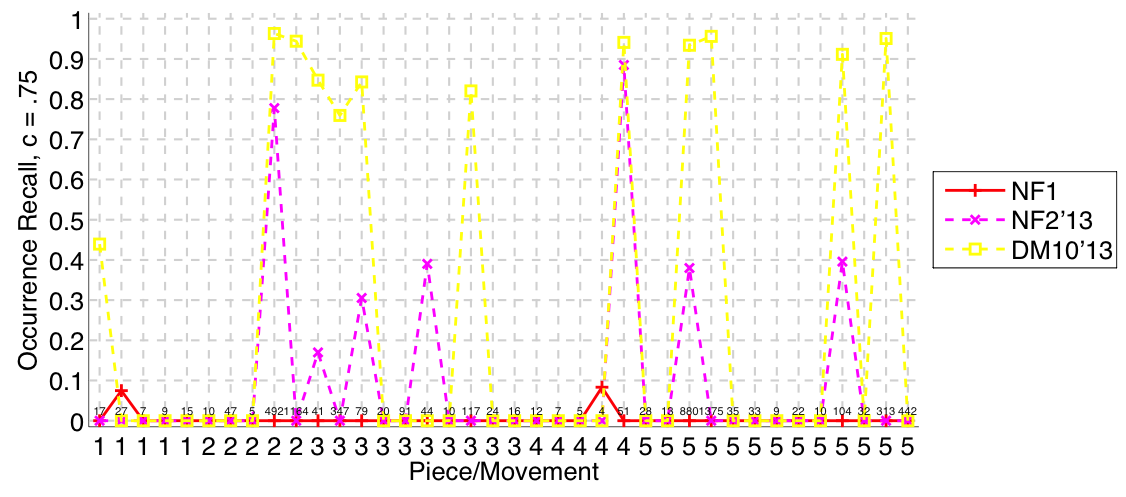
Figure 3. Occurrence recall on a per-pattern basis. Occurrence recall answers the following question. On average, how similar is the most similar set of algorithm-output pattern occurrences to a discovered ground-truth occurrence set?

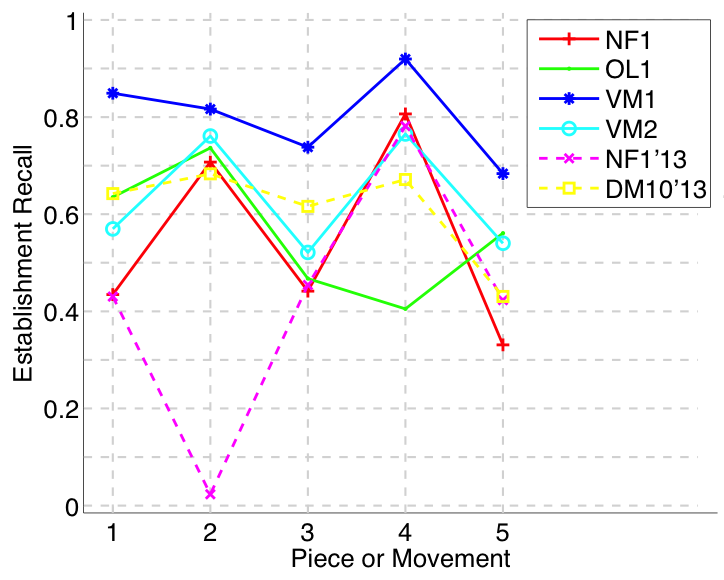
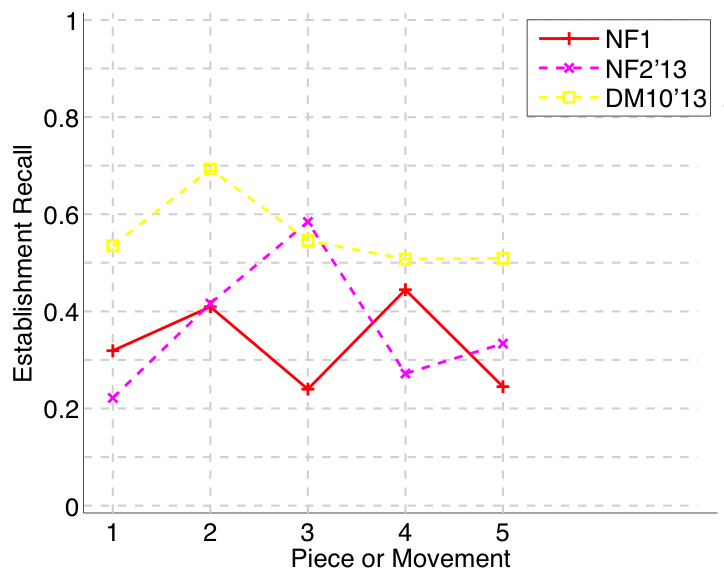
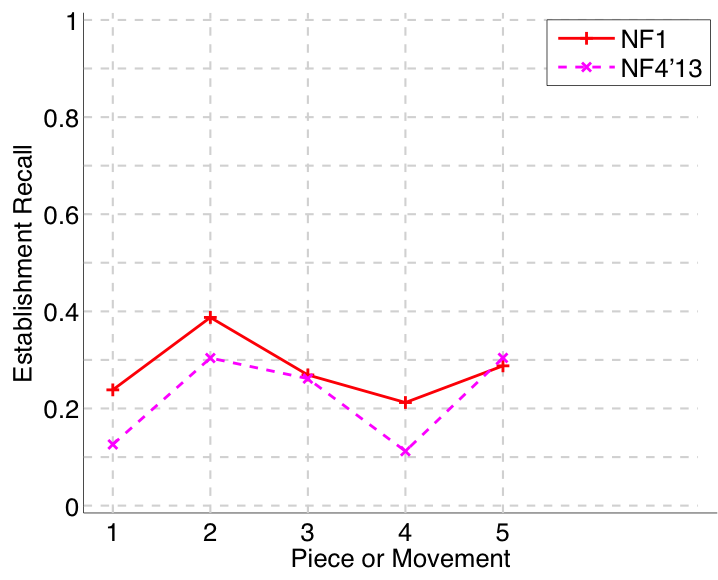
Figure 4. Establishment recall averaged over each piece/movement. Establishment recall answers the following question. On average, how similar is the most similar algorithm-output pattern to a ground-truth pattern prototype?

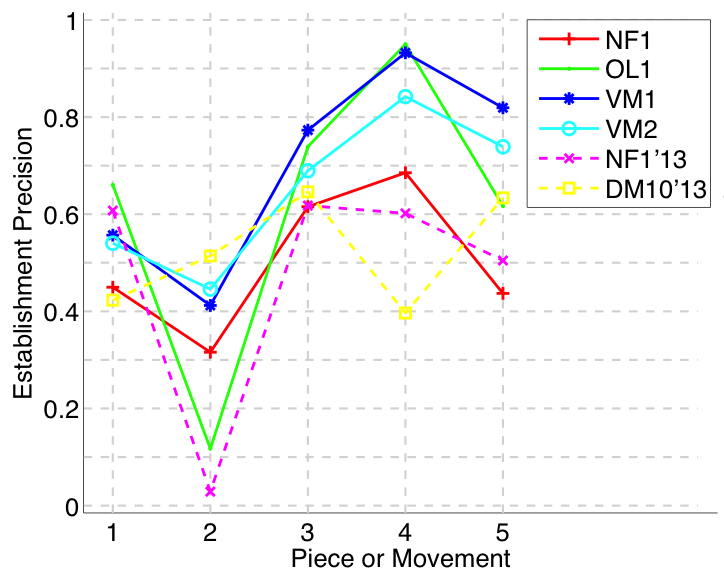
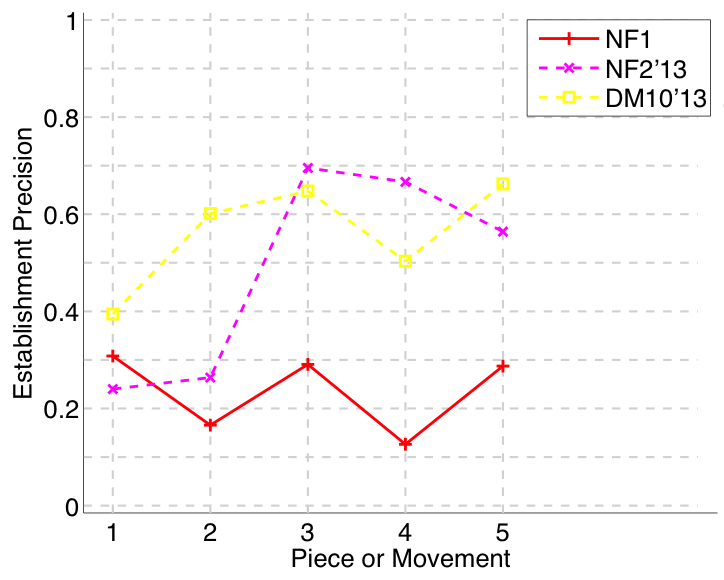
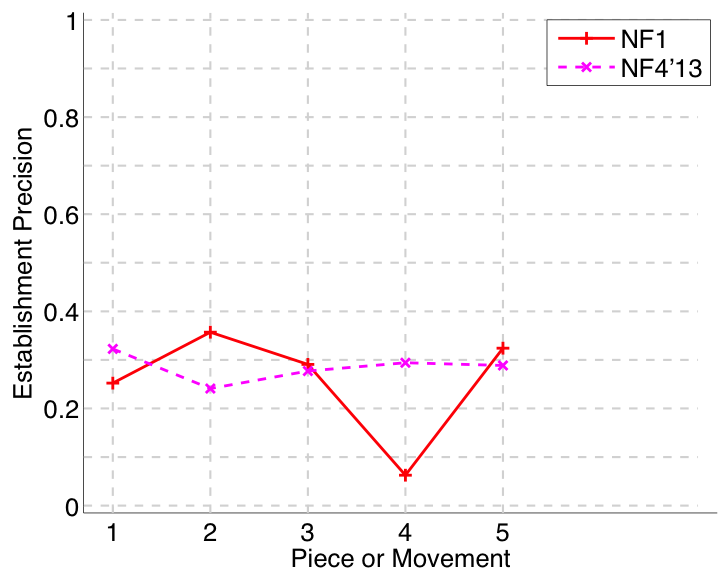
Figure 5. Establishment precision averaged over each piece/movement. Establishment precision answers the following question. On average, how similar is the most similar ground-truth pattern prototype to an algorithm-output pattern?

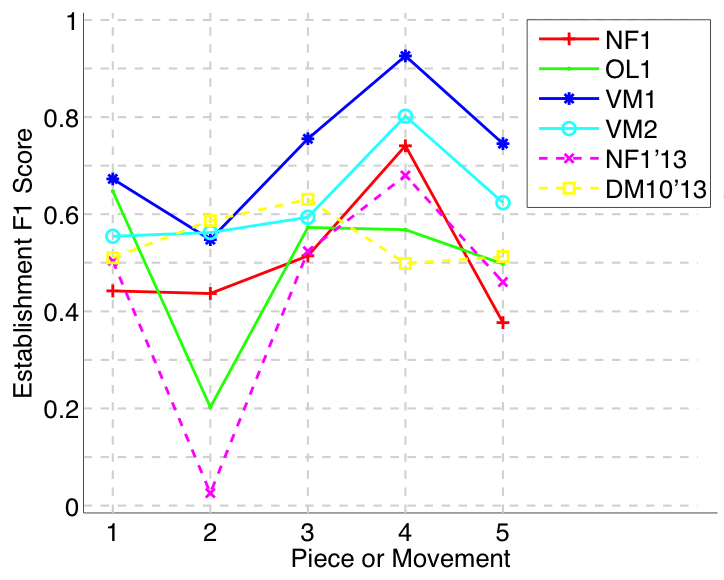
Figure 6. Establishment F1 averaged over each piece/movement. Establishment F1 is an average of establishment precision and establishment recall.

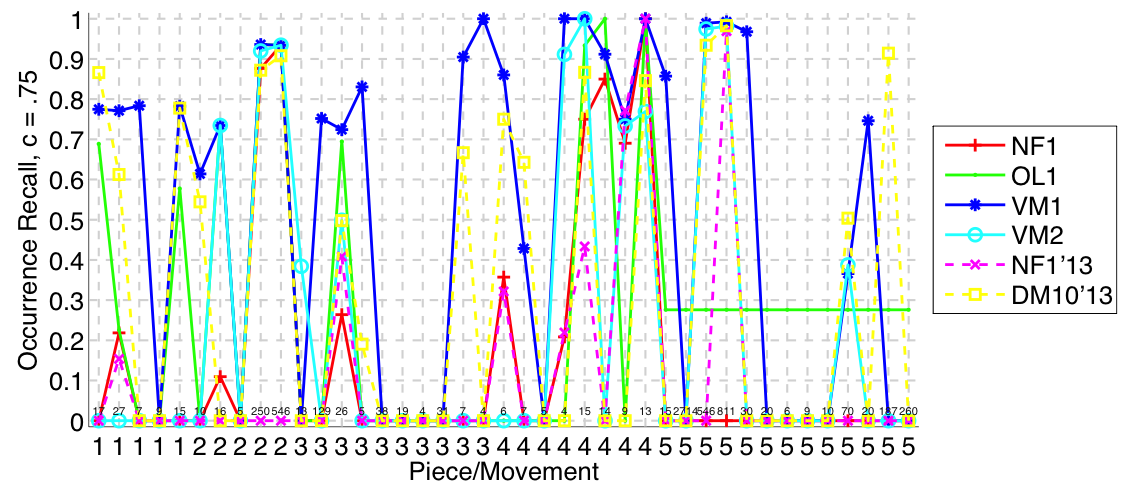
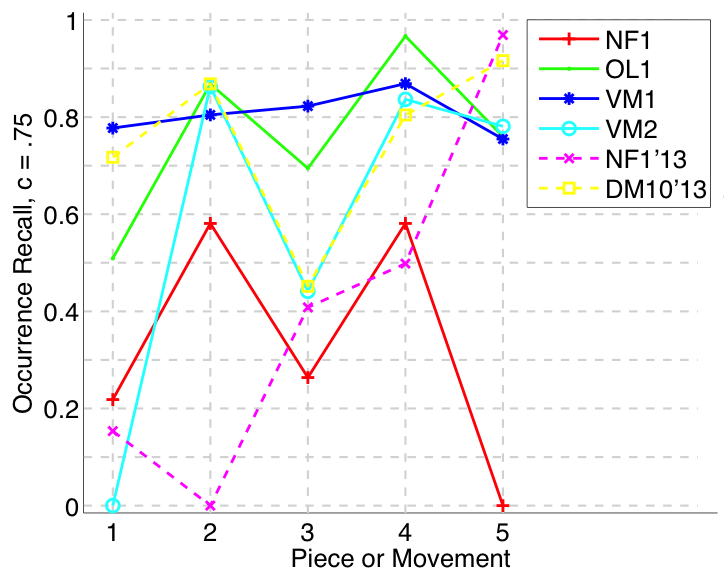
Figure 7. Occurrence recall ( $c=.75$ ) averaged over each piece/movement. Occurrence recall answers the following question. On average, how similar is the most similar set of algorithm-output pattern occurrences to a discovered ground-truth occurrence set?

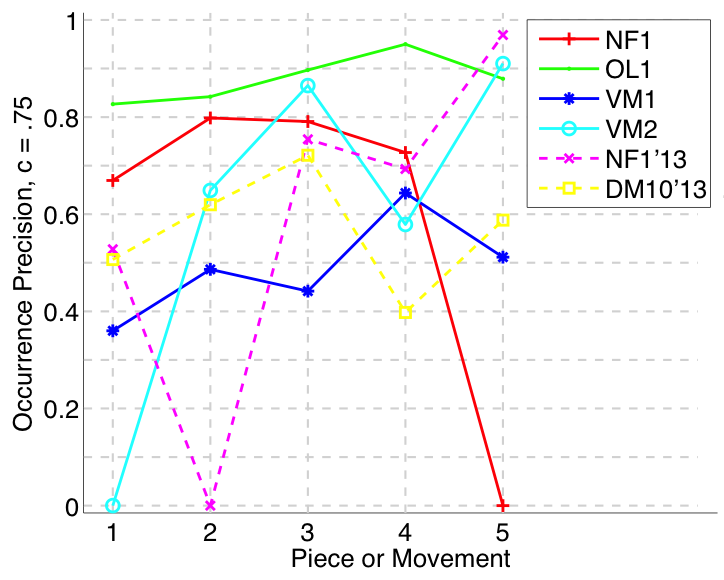
Figure 8. Occurrence precision ( $c=.75$ ) averaged over each piece/movement. Occurrence precision answers the following question. On average, how similar is the most similar discovered ground-truth occurrence set to a set of algorithm-output pattern occurrences?

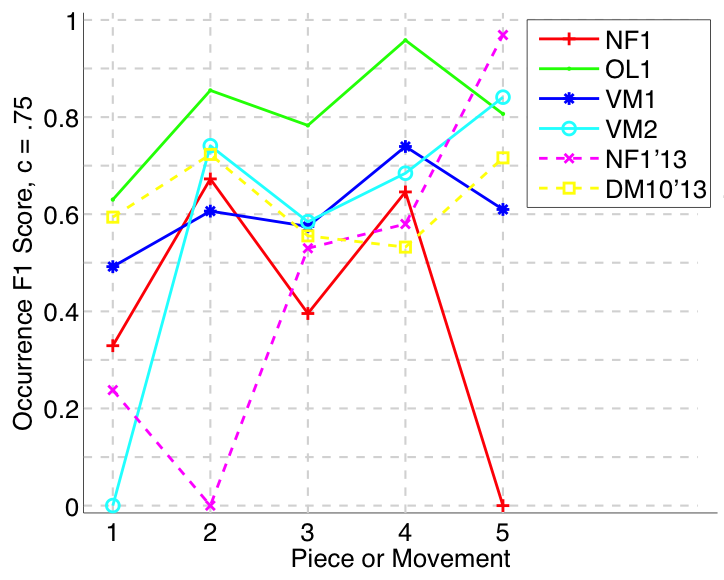
Figure 9. Occurrence F1 ( $c=.75$ ) averaged over each piece/movement. Occurrence F1 is an average of occurrence precision and occurrence recall.

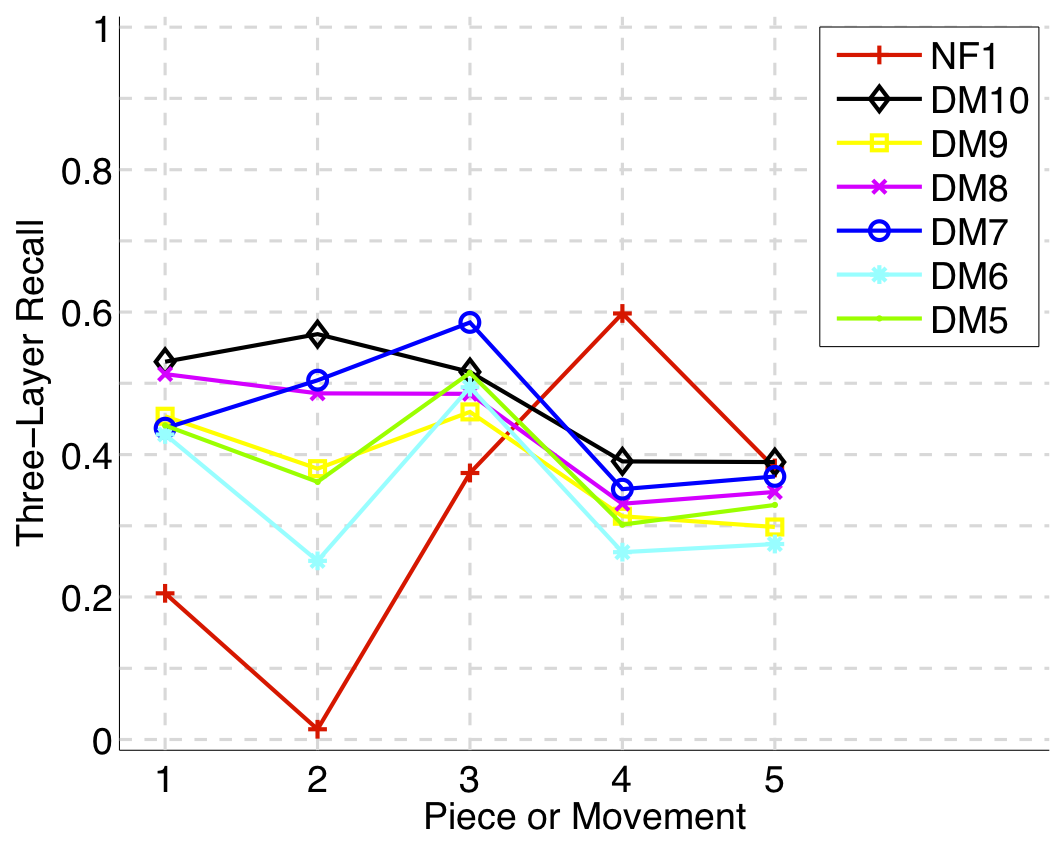
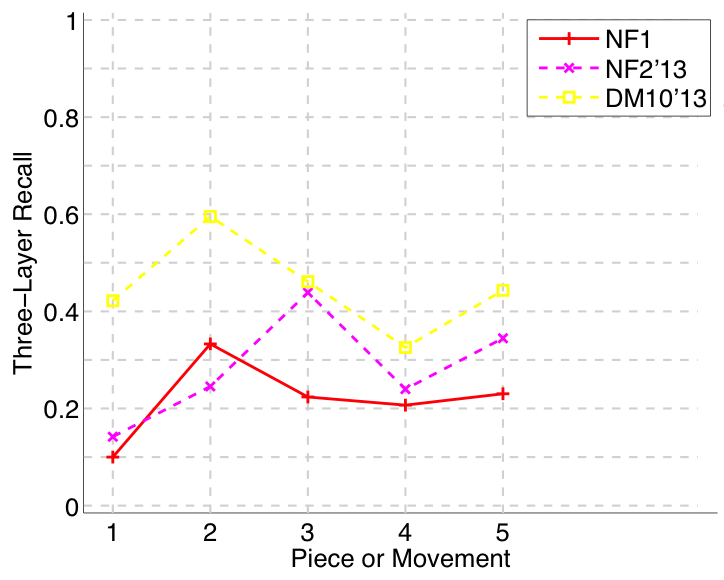
Figure 10. Three-layer recall averaged over each piece/movement. Rather than using $|P\cap Q|/\max\{|P|,|Q|\}$ as a similarity measure (which is the default for establishment recall), three-layer recall uses $2|P\cap Q|/(|P|+|Q|)$ , which is a kind of F1 measure.

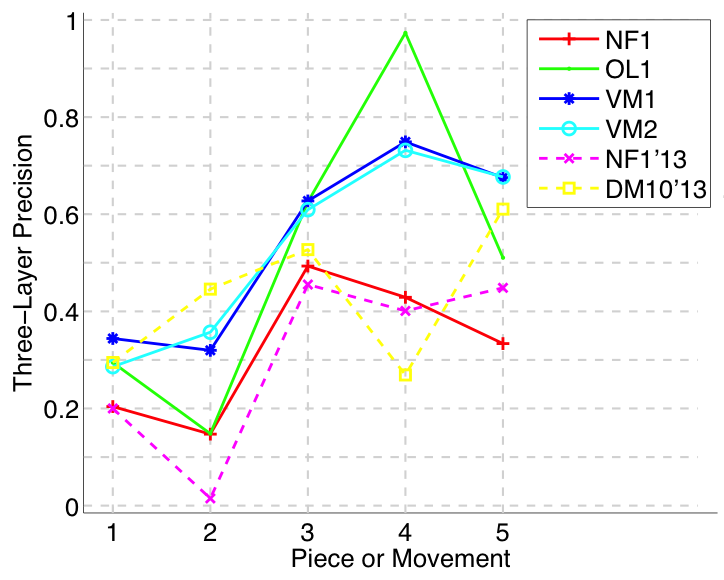
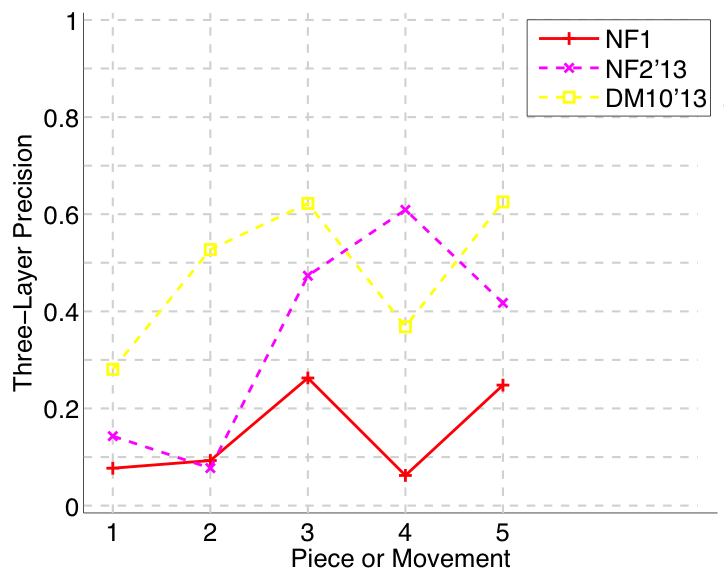
Figure 11. Three-layer precision averaged over each piece/movement. Rather than using $|P\cap Q|/\max\{|P|,|Q|\}$ as a similarity measure (which is the default for establishment precision), three-layer precision uses $2|P\cap Q|/(|P|+|Q|)$ , which is a kind of F1 measure.

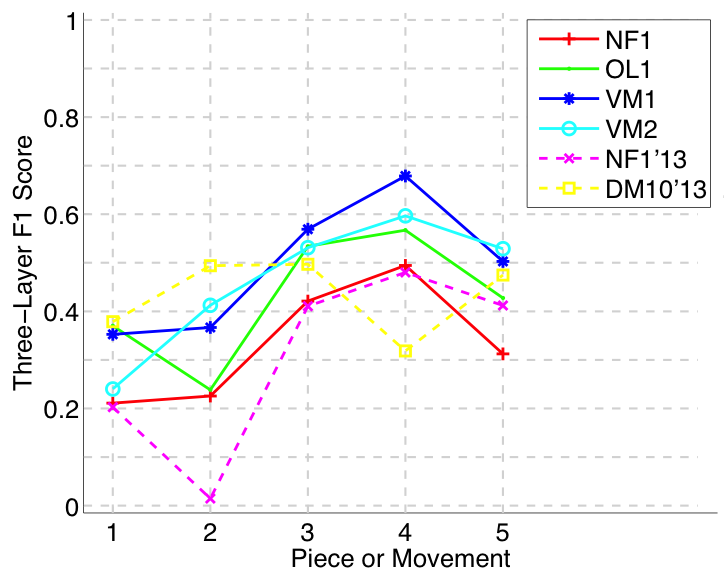
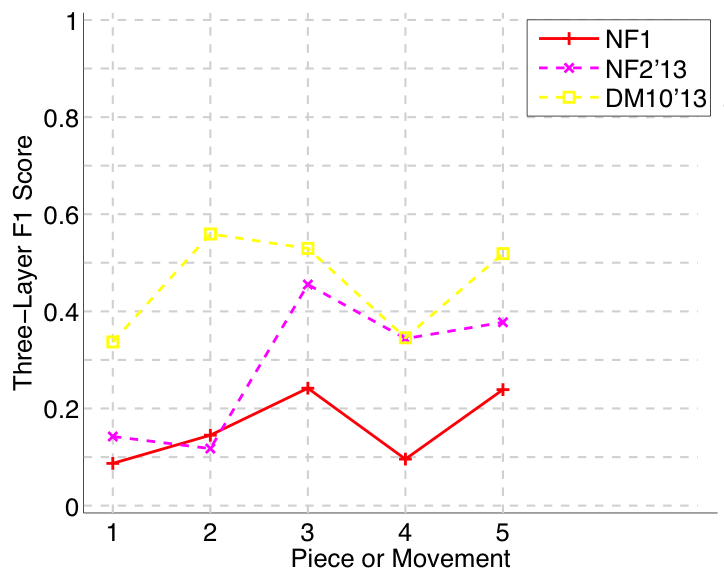
Figure 12. Three-layer F1 (TLF) averaged over each piece/movement. TLF is an average of three-layer precision and three-layer recall.

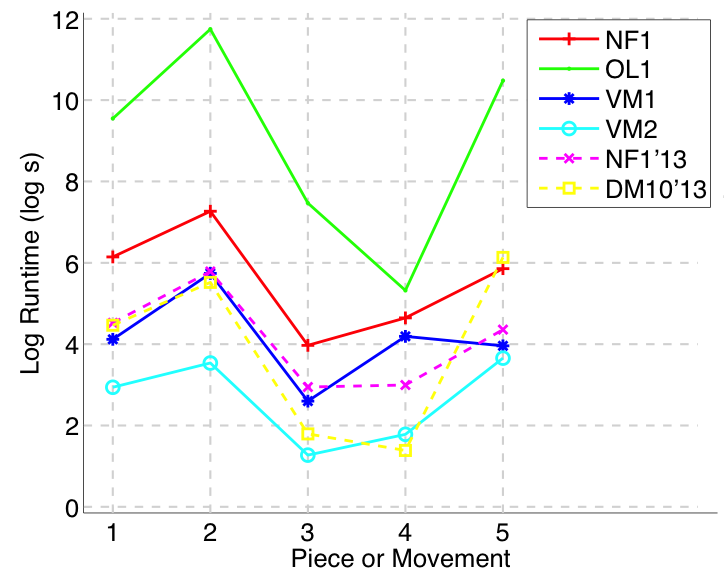
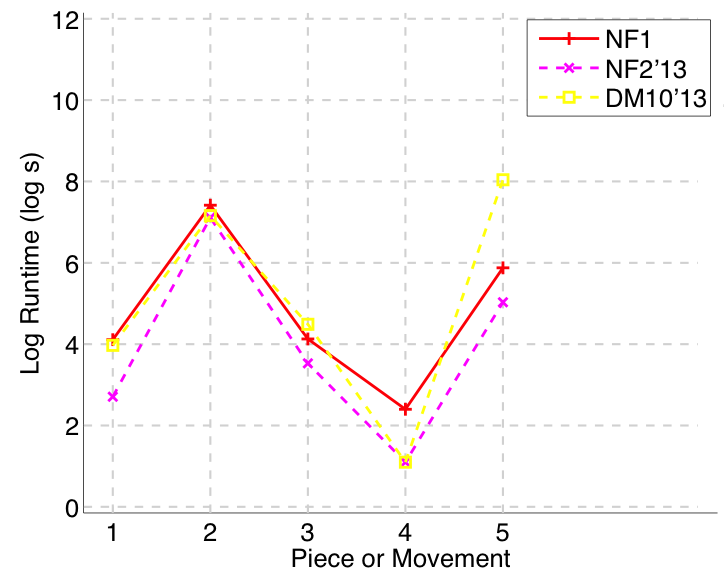
Figure 13. Log runtime of the algorithm for each piece/movement.

symPoly

Figure 14. Establishment recall on a per-pattern basis. Establishment recall answers the following question. On average, how similar is the most similar algorithm-output pattern to a ground-truth pattern prototype?

Figure 15. Occurrence recall on a per-pattern basis. Occurrence recall answers the following question. On average, how similar is the most similar set of algorithm-output pattern occurrences to a discovered ground-truth occurrence set?

Figure 16. Establishment recall averaged over each piece/movement. Establishment recall answers the following question. On average, how similar is the most similar algorithm-output pattern to a ground-truth pattern prototype?

Figure 17. Establishment precision averaged over each piece/movement. Establishment precision answers the following question. On average, how similar is the most similar ground-truth pattern prototype to an algorithm-output pattern?

Figure 18. Establishment F1 averaged over each piece/movement. Establishment F1 is an average of establishment precision and establishment recall.

Figure 19. Occurrence recall ( $c=.75$ ) averaged over each piece/movement. Occurrence recall answers the following question. On average, how similar is the most similar set of algorithm-output pattern occurrences to a discovered ground-truth occurrence set?

Figure 20. Occurrence precision ( $c=.75$ ) averaged over each piece/movement. Occurrence precision answers the following question. On average, how similar is the most similar discovered ground-truth occurrence set to a set of algorithm-output pattern occurrences?

Figure 21. Occurrence F1 ( $c=.75$ ) averaged over each piece/movement. Occurrence F1 is an average of occurrence precision and occurrence recall.

Figure 22. Three-layer recall averaged over each piece/movement. Rather than using $|P\cap Q|/\max\{|P|,|Q|\}$ as a similarity measure (which is the default for establishment recall), three-layer recall uses $2|P\cap Q|/(|P|+|Q|)$ , which is a kind of F1 measure.

Figure 23. Three-layer precision averaged over each piece/movement. Rather than using $|P\cap Q|/\max\{|P|,|Q|\}$ as a similarity measure (which is the default for establishment precision), three-layer precision uses $2|P\cap Q|/(|P|+|Q|)$ , which is a kind of F1 measure.

Figure 24. Three-layer F1 (TLF) averaged over each piece/movement. TLF is an average of three-layer precision and three-layer recall.

Figure 25. Log runtime of the algorithm for each piece/movement.

audMono

Figure 26. Establishment recall on a per-pattern basis. Establishment recall answers the following question. On average, how similar is the most similar algorithm-output pattern to a ground-truth pattern prototype?

Figure 27. Occurrence recall on a per-pattern basis. Occurrence recall answers the following question. On average, how similar is the most similar set of algorithm-output pattern occurrences to a discovered ground-truth occurrence set?

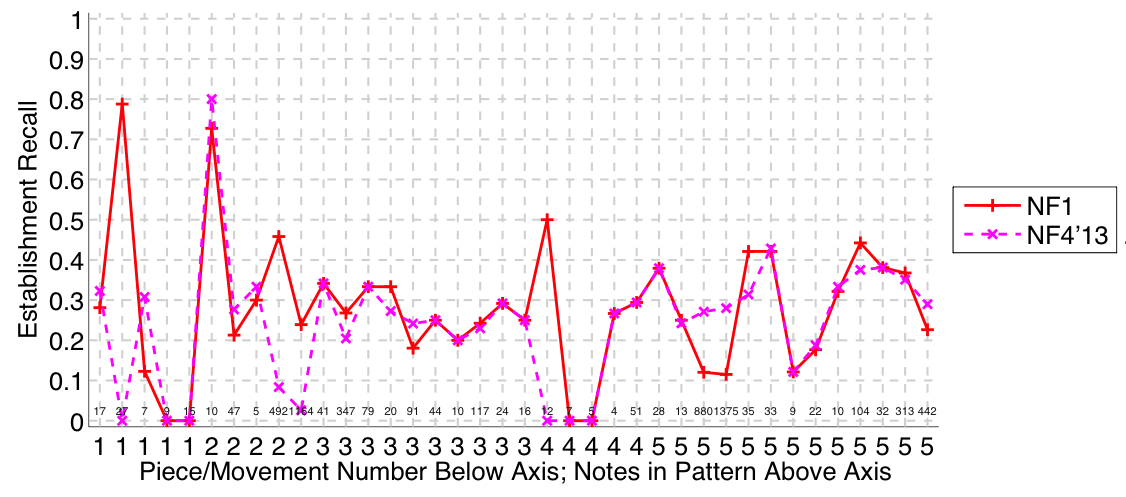
Figure 28. Establishment recall averaged over each piece/movement. Establishment recall answers the following question. On average, how similar is the most similar algorithm-output pattern to a ground-truth pattern prototype?

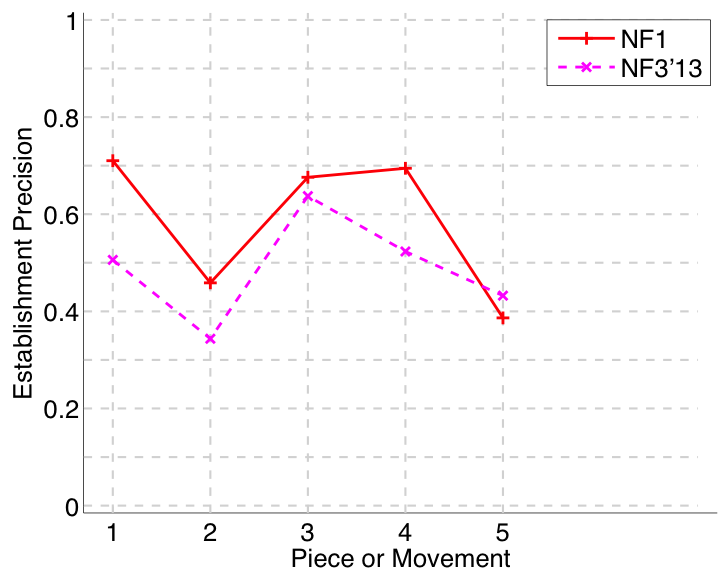
Figure 29. Establishment precision averaged over each piece/movement. Establishment precision answers the following question. On average, how similar is the most similar ground-truth pattern prototype to an algorithm-output pattern?

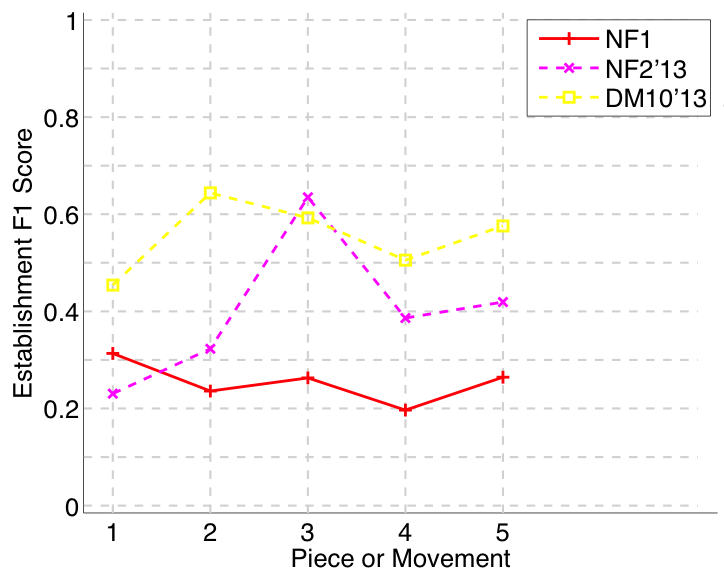
Figure 30. Establishment F1 averaged over each piece/movement. Establishment F1 is an average of establishment precision and establishment recall.

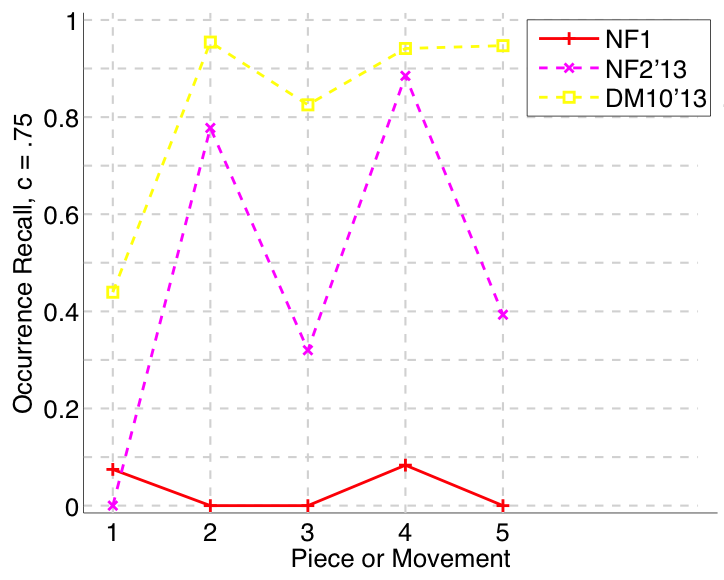
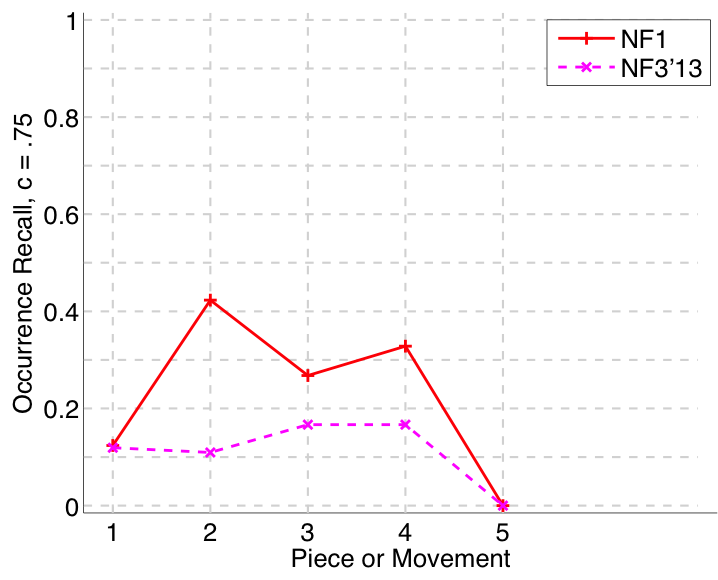
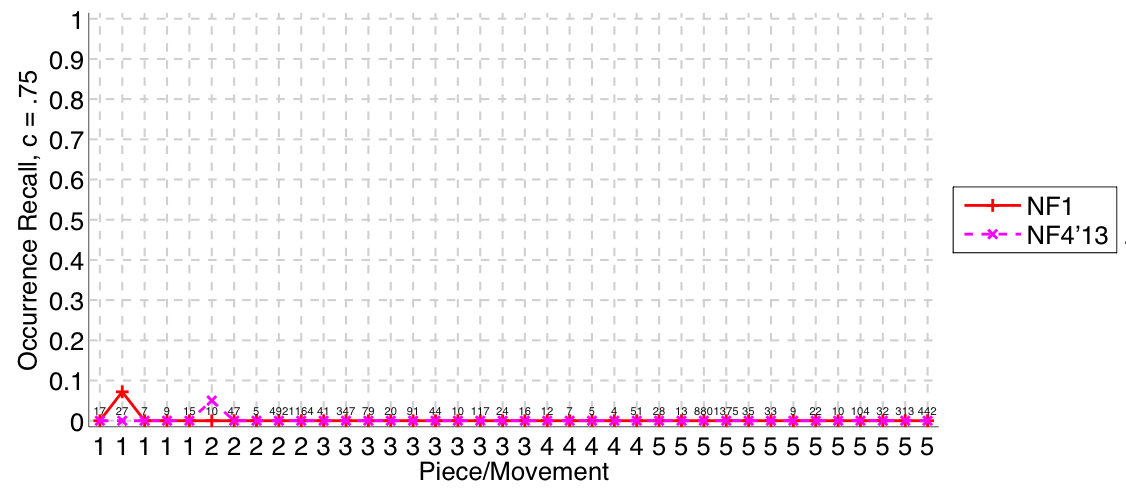
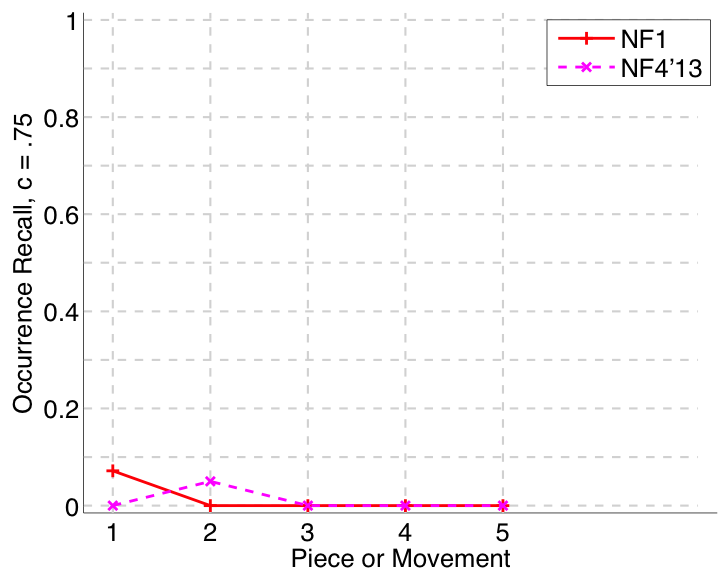
Figure 31. Occurrence recall ( $c=.75$ ) averaged over each piece/movement. Occurrence recall answers the following question. On average, how similar is the most similar set of algorithm-output pattern occurrences to a discovered ground-truth occurrence set?

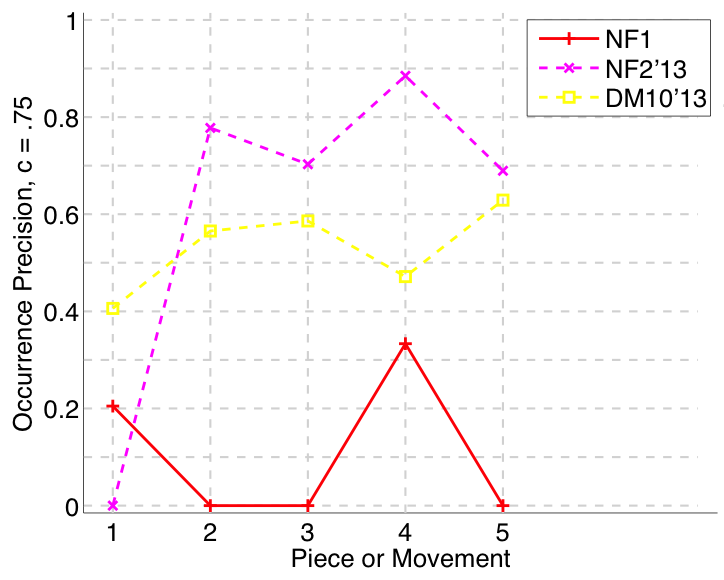
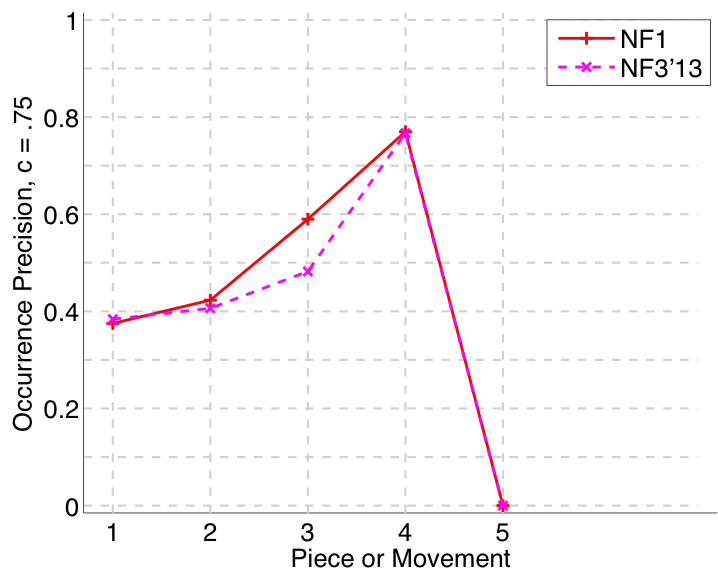
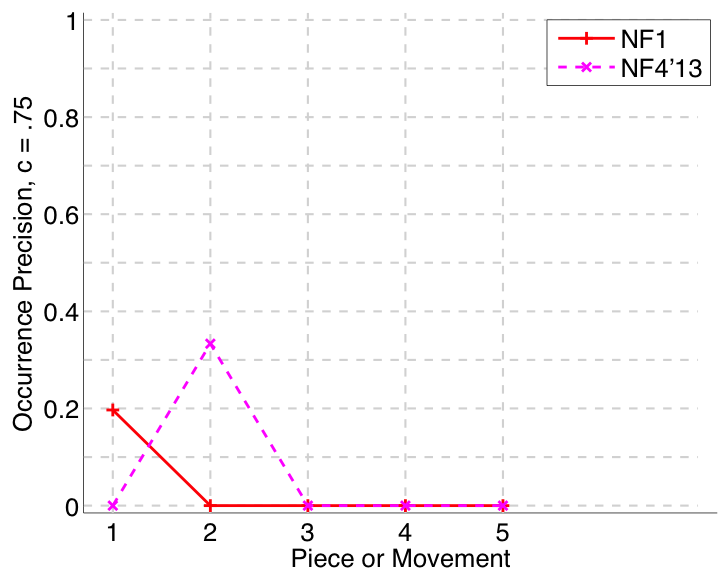
Figure 32. Occurrence precision ( $c=.75$ ) averaged over each piece/movement. Occurrence precision answers the following question. On average, how similar is the most similar discovered ground-truth occurrence set to a set of algorithm-output pattern occurrences?

Figure 33. Occurrence F1 ( $c=.75$ ) averaged over each piece/movement. Occurrence F1 is an average of occurrence precision and occurrence recall.

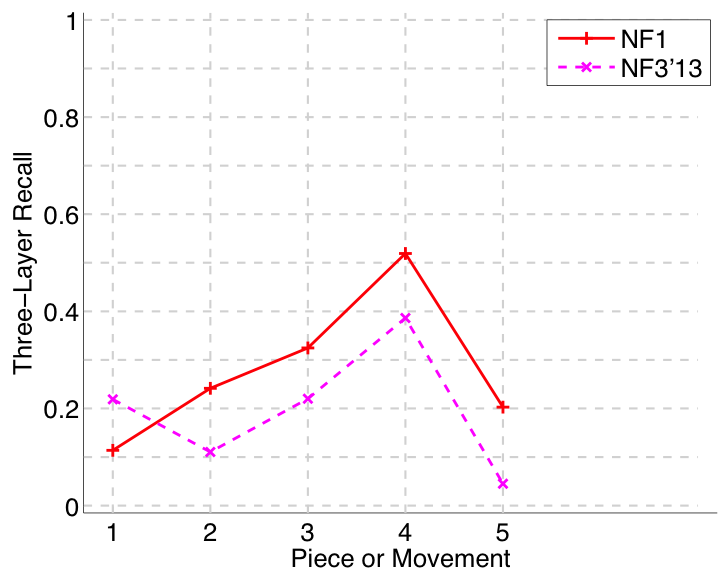
Figure 34. Three-layer recall averaged over each piece/movement. Rather than using $|P\cap Q|/\max\{|P|,|Q|\}$ as a similarity measure (which is the default for establishment recall), three-layer recall uses $2|P\cap Q|/(|P|+|Q|)$ , which is a kind of F1 measure.

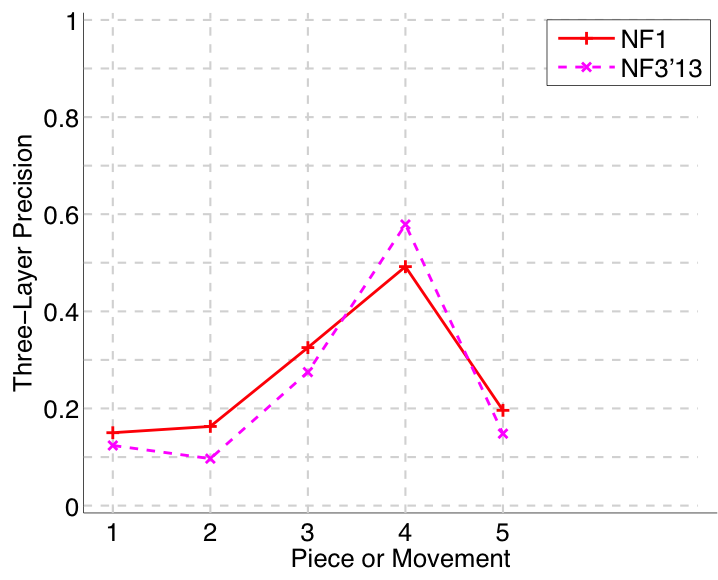
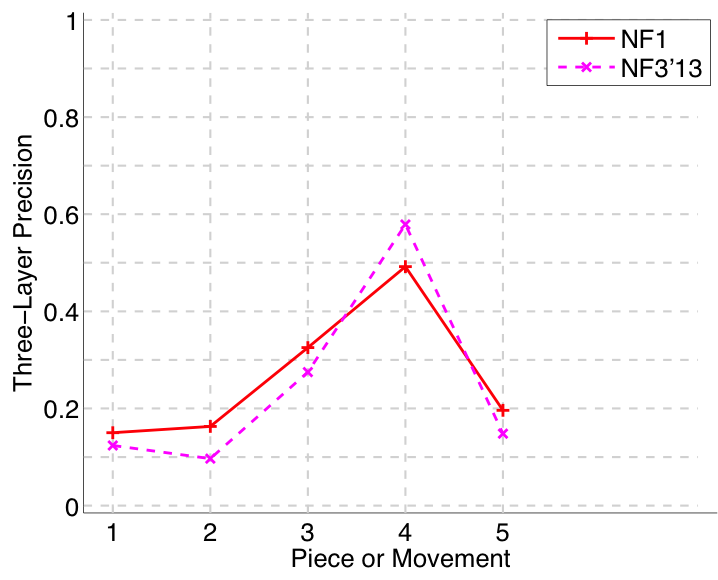
Figure 35. Three-layer precision averaged over each piece/movement. Rather than using $|P\cap Q|/\max\{|P|,|Q|\}$ as a similarity measure (which is the default for establishment precision), three-layer precision uses $2|P\cap Q|/(|P|+|Q|)$ , which is a kind of F1 measure.

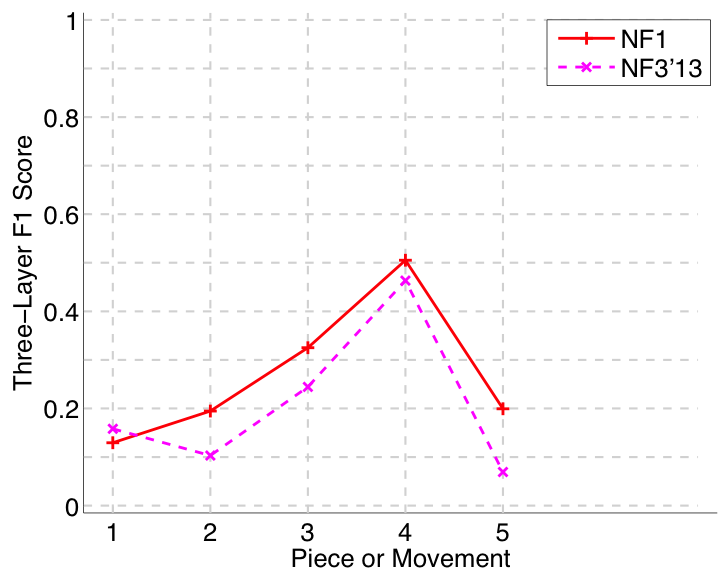
Figure 36. Three-layer F1 (TLF) averaged over each piece/movement. TLF is an average of three-layer precision and three-layer recall.

Figure 37. Log runtime of the algorithm for each piece/movement.

audPoly

Figure 38. Establishment recall on a per-pattern basis. Establishment recall answers the following question. On average, how similar is the most similar algorithm-output pattern to a ground-truth pattern prototype?

Figure 39. Occurrence recall on a per-pattern basis. Occurrence recall answers the following question. On average, how similar is the most similar set of algorithm-output pattern occurrences to a discovered ground-truth occurrence set?

Figure 40. Establishment recall averaged over each piece/movement. Establishment recall answers the following question. On average, how similar is the most similar algorithm-output pattern to a ground-truth pattern prototype?

Figure 41. Establishment precision averaged over each piece/movement. Establishment precision answers the following question. On average, how similar is the most similar ground-truth pattern prototype to an algorithm-output pattern?

Figure 42. Establishment F1 averaged over each piece/movement. Establishment F1 is an average of establishment precision and establishment recall.

Figure 43. Occurrence recall ( $c=.75$ ) averaged over each piece/movement. Occurrence recall answers the following question. On average, how similar is the most similar set of algorithm-output pattern occurrences to a discovered ground-truth occurrence set?

Figure 44. Occurrence precision ( $c=.75$ ) averaged over each piece/movement. Occurrence precision answers the following question. On average, how similar is the most similar discovered ground-truth occurrence set to a set of algorithm-output pattern occurrences?

Figure 45. Occurrence F1 ( $c=.75$ ) averaged over each piece/movement. Occurrence F1 is an average of occurrence precision and occurrence recall.

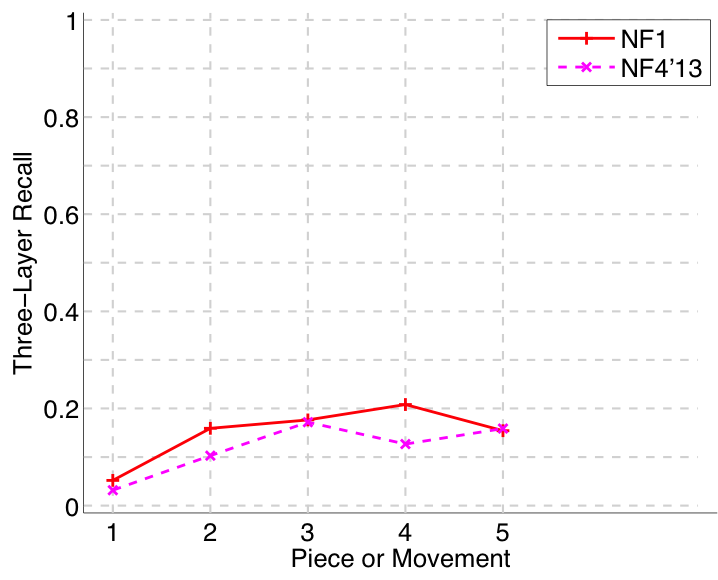
Figure 46. Three-layer recall averaged over each piece/movement. Rather than using $|P\cap Q|/\max\{|P|,|Q|\}$ as a similarity measure (which is the default for establishment recall), three-layer recall uses $2|P\cap Q|/(|P|+|Q|)$ , which is a kind of F1 measure.

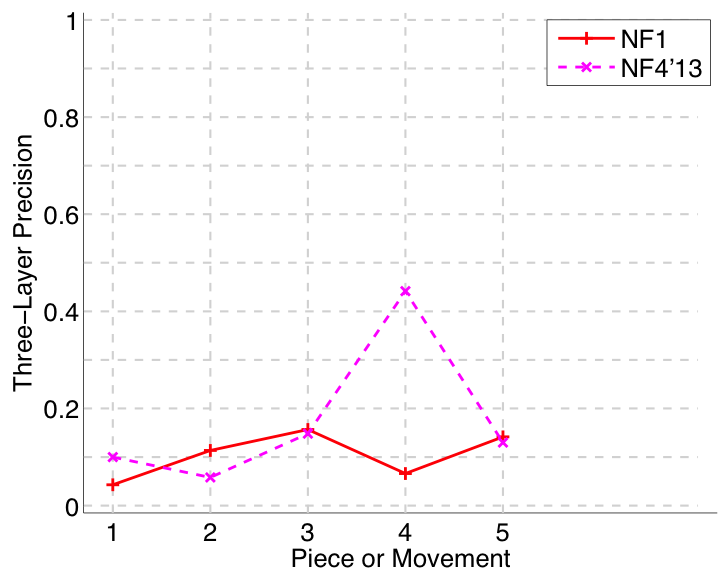
Figure 47. Three-layer precision averaged over each piece/movement. Rather than using $|P\cap Q|/\max\{|P|,|Q|\}$ as a similarity measure (which is the default for establishment precision), three-layer precision uses $2|P\cap Q|/(|P|+|Q|)$ , which is a kind of F1 measure.

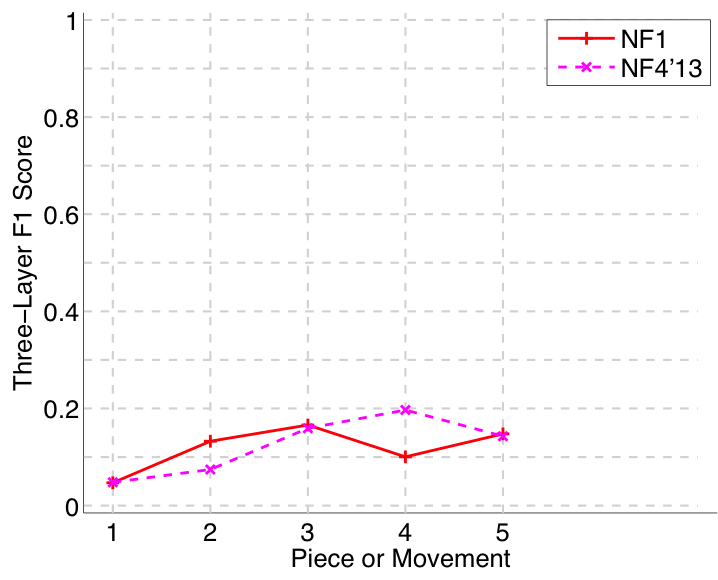
Figure 48. Three-layer F1 (TLF) averaged over each piece/movement. TLF is an average of three-layer precision and three-layer recall.

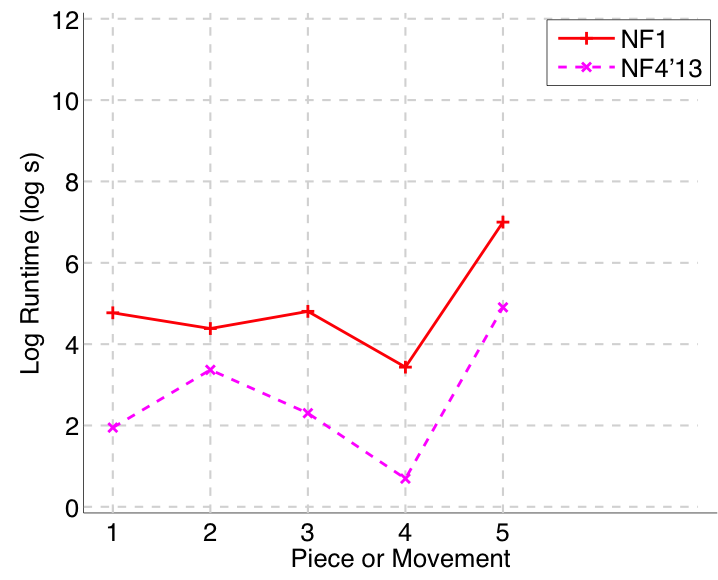
Figure 49. Log runtime of the algorithm for each piece/movement.

Discussion

If an occurrence of a ground-truth pattern contains forty or more notes then, according to Fig. 2, it is likely that SIATECSegment (DM10, Meredith, 2013) and motives_poly (NF2, Nieto & Farbood, 2013) will return a pattern rated as at least 75% similar. When we restrict attention to these successful discoveries and ask to what extent can the algorithms retrieve all exact and inexact occurrences, we find that SIATECSegment performs relatively well (see nonzero entries for the black line in Fig. 3), with the exception of the first patterns in pieces 1 and 2. We conclude, therefore, that the discovery of repeated sections has been addressed well by the current submissions, but that the discovery of themes and motifs requires more attention in future iterations of this task.

When assembling the ground truth, it was remarkable that most often a motif occurs as a subset of a theme or repeated section, which is not surprising given Drabkin’s (2001) definition of a motif as ‘the shortest subdivision of a theme or phrase that still maintains its identity as an idea’. One suggestion for future work is to apply a discovery algorithm to find repeated sections, and then apply the algorithm again but to the output sections only, in order to retrieve these nested and important musical motifs.